- Record: found
- Abstract: found
- Article: not found
Efficient Bayesian mixed model analysis increases association power in large cohorts
research-article
Author(s):
Po-Ru Loh
1
,
2 ,
George Tucker
1
,
3
,
4 ,
Brendan K Bulik-Sullivan
2
,
5 ,
Bjarni J Vilhjálmsson
1
,
2 ,
Hilary K Finucane
3 ,
Rany M Salem
2
,
6 ,
Daniel I Chasman
7 ,
Paul M Ridker
7 ,
Benjamin M Neale
2
,
5 ,
Bonnie Berger
3
,
4 ,
Nick Patterson
2 ,
Alkes L Price
1
,
2
,
8
Publication date (Electronic):
02 February 2015
Journal:
Nature genetics
There is no author summary for this article yet. Authors can add summaries to their articles on ScienceOpen to make them more accessible to a non-specialist audience.
Abstract
Linear mixed models are a powerful statistical tool for identifying genetic associations and avoiding confounding. However, existing methods are computationally intractable in large cohorts, and may not optimize power. All existing methods require time cost O(MN 2) (where N = #samples and M = #SNPs) and implicitly assume an infinitesimal genetic architecture in which effect sizes are normally distributed, which can limit power. Here, we present a far more efficient mixed model association method, BOLT-LMM, which requires only a small number of O(MN)-time iterations and increases power by modeling more realistic, non-infinitesimal genetic architectures via a Bayesian mixture prior on marker effect sizes. We applied BOLT-LMM to nine quantitative traits in 23,294 samples from the Women’s Genome Health Study (WGHS) and observed significant increases in power, consistent with simulations. Theory and simulations show that the boost in power increases with cohort size, making BOLT-LMM appealing for GWAS in large cohorts.
Related collections
Most cited references39
- Record: found
- Abstract: found
- Article: not found
An efficient multi-locus mixed model approach for genome-wide association studies in structured populations
Population structure causes genome-wide linkage disequilibrium between unlinked loci, leading to statistical confounding in genome-wide association studies. Mixed models have been shown to handle the confounding effects of a diffuse background of large numbers of loci of small effect well, but do not always account for loci of larger effect. Here we propose a multi-locus mixed model as a general method for mapping complex traits in structured populations. Simulations suggest that our method outperforms existing methods, in terms of power as well as false discovery rate. We apply our method to human and Arabidopsis thaliana data, identifying novel associations in known candidates as well as evidence for allelic heterogeneity. We also demonstrate how a priori knowledge from an A. thaliana linkage mapping study can be integrated into our method using a Bayesian approach. Our implementation is computationally efficient, making the analysis of large datasets (n > 10000) practicable.
- Record: found
- Abstract: found
- Article: found
Polygenic Modeling with Bayesian Sparse Linear Mixed Models
Xiang Zhou, Peter Carbonetto, Matthew Stephens (2013)
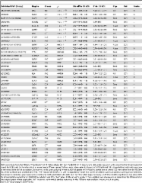
Introduction Both linear mixed models (LMMs) and sparse regression models are widely used in genetics applications. For example, LMMs are often used to control for population stratification, individual relatedness, or unmeasured confounding factors when performing association tests in genetic association studies [1]–[9] and gene expression studies [10]–[12]. They have also been used in genetic association studies to jointly analyze groups of SNPs [13], [14]. Similarly, sparse regression models have been used in genome-wide association analyses [15]–[20] and in expression QTL analysis [21]. Further, both LMMs and sparse regression models have been applied to, and garnered renewed interest in, polygenic modeling in association studies. Here, by polygenic modeling we mean any attempt to relate phenotypic variation to many genetic variants simultaneously (in contrast to single-SNP tests of association). The particular polygenic modeling problems that we focus on here are estimating “chip heritability”, being the proportion of variance in phenotypes explained (PVE) by available genotypes [19], [22]–[24], and predicting phenotypes based on genotypes [25]–[29]. Despite the considerable overlap in their applications, in the context of polygenic modeling, LMMs and sparse regression models are based on almost diametrically opposed assumptions. Precisely, applications of LMMs to polygenic modeling (e.g. [22]) effectively assume that every genetic variant affects the phenotype, with effect sizes normally distributed, whereas sparse regression models, such as Bayesian variable selection regression models (BVSR) [18], [19], assume that a relatively small proportion of all variants affect the phenotype. The relative performance of these two models for polygenic modeling applications would therefore be expected to vary depending on the true underlying genetic architecture of the phenotype. However, in practice, one does not know the true genetic architecture, so it is unclear which of the two models to prefer. Motivated by this observation, we consider a hybrid of these two models, which we refer to as the “Bayesian sparse linear mixed model”, or BSLMM. This hybrid includes both the LMM and a sparse regression model, BVSR, as special cases, and is to some extent capable of learning the genetic architecture from the data, yielding good performance across a wide range of scenarios. By being “adaptive” to the data in this way, our approach obviates the need to choose one model over the other, and attempts to combine the benefits of both. The idea of a hybrid between LMM and sparse regression models is, in itself, not new. Indeed, models like these have been used in breeding value prediction to assist genomic selection in animal and plant breeding programs [30]–[35], gene selection in expression analysis while controlling for batch effects [36], phenotype prediction of complex traits in model organisms and dairy cattle [37]–[40], and more recently, mapping complex traits by jointly modeling all SNPs in structured populations [41]. Compared with these previous papers, our work makes two key contributions. First, we consider in detail the specification of appropriate prior distributions for the hyper-parameters of the model. We particularly emphasize the benefits of estimating the hyper-parameters from the data, rather than fixing them to pre-specified values to achieve the adaptive behavior mentioned above. Second, we provide a novel computational algorithm that exploits a recently described linear algebra trick for LMMs [8], [9]. The resulting algorithm avoids ad hoc approximations that are sometimes made when fitting these types of model (e.g. [37], [41]), and yields reliable results for datasets containing thousands of individuals and hundreds of thousands of markers. (Most previous applications of this kind of model involved much smaller datasets.) Since BSLMM is a hybrid of two widely used models, it naturally has a wide range of potential uses. Here we focus on its application to polygenic modeling for genome-wide association studies, specifically two applications of particular interest and importance: PVE estimation (or “chip heritability” estimation) and phenotype prediction. Estimating the PVE from large-scale genotyped marker sets (e.g. all the SNPs on a genome-wide genotyping chip) has the potential to shed light on sources of “missing heritability” [42] and the underlying genetic architecture of common diseases [19], [22]–[24], [43]. And accurate prediction of complex phenotypes from genotypes could ultimately impact many areas of genetics, including applications in animal breeding, medicine and forensics [27]–[29], [37]–[40]. Through simulations and applications to real data, we show that BSLMM successfully combines the advantages of both LMMs and sparse regression, is robust to a variety of settings in PVE estimation, and outperforms both models, and several related models, in phenotype prediction. Methods Background and Motivation We begin by considering a simple linear model relating phenotypes to genotypes : (1) (2) Here is an -vector of phenotypes measured on individuals, is an matrix of genotypes measured on the same individuals at genetic markers, is a -vector of (unknown) genetic marker effects, is an -vector of 1 s, is a scalar representing the phenotype mean, and is an -vector of error terms that have variance . denotes the -dimensional multivariate normal distribution. Note that there are many ways in which measured genotypes can be encoded in the matrix . We assume throughout this paper that the genotypes are coded as 0, 1 or 2 copies of a reference allele at each marker, and that the columns of are centered but not standardized; see Text S1. A key issue is that, in typical current datasets (e.g. GWAS), the number of markers is much larger than the number of individuals . As a result, parameters of interest (e.g. or PVE) cannot be estimated accurately without making some kind of modeling assumptions. Indeed, many existing approaches to polygenic modeling can be derived from (1) by making specific assumptions about the genetic effects . For example, the LMM approach from [22], which has recently become commonly used for PVE estimation (e.g. [24], [44]–[46]), is equivalent to the assumption that effect sizes are normally distributed, such that (3) [Specifically, exact equivalence holds when the relatedness matrix in the LMM is computed from the genotypes as (e.g. [47]). [22] use a matrix in this form, with centered and standardized, and with a slight modification of the diagonal elements.] For brevity, in this paper we refer to the regression model that results from this assumption as the LMM (note that this is relatively restrictive compared with the usual definition); it is also commonly referred to as “ridge regression” in statistics [48]. The estimated combined effects ( ), or equivalently, the estimated random effects, obtained from this model are commonly referred to as Best Linear Unbiased Predictors (BLUP) [49]. An alternative assumption, which has also been widely used in polygenic modeling applications [18], [19], [34], and more generally in statistics for sparse high-dimensional regression with large numbers of covariates [50], [51], is that the effects come from a mixture of a normal distribution and a point mass at 0, also known as a point-normal distribution: (4) where is the proportion of non-zero and denotes a point mass at zero. [This definition of follows the convention from statistics [19], [50], [51], which is opposite to the convention in animal breeding [27], [32]–[34], [40].] We refer to the resulting regression model as Bayesian Variable Selection Regression (BVSR), because it is commonly used to select the relevant variables (i.e. those with non-zero effect) for phenotype prediction. Although (4) formally includes (3) as a special case when , in practice (4) is often used together with an assumption that only a small proportion of the variables are likely to be relevant for phenotype prediction, say by specifying a prior distribution for that puts appreciable mass on small values (e.g. [19]). In this case, BVSR and LMM can be viewed as making almost diametrically opposed assumptions: the LMM assumes every variant has an effect, whereas BVSR assumes that a very small proportion of variants have an effect. (In practice, the estimate of under LMM is often smaller than the estimate of under BVSR, so we can interpret the LMM as assuming a large number of small effects, and BVSR as assuming a small number of larger effects.) A more general assumption, which includes both the above as special cases, is that the effects come from a mixture of two normal distributions: (5) Setting yields the LMM (3), and yields BVSR (4). we can interpret this model as assuming that all variants have at least a small effect, which are normally distributed with variance , and some proportion ( ) of variants have an additional effect, normally distributed with variance . The earliest use of a mixture of two normal distributions for the regression coefficients that we are aware of is [52], although in that paper various hyper-parameters were fixed, and so it did not include LMM and BVSR as special cases. Of the three assumptions on the effect size distributions above, the last (5) is clearly the most flexible since it includes the others as special cases. Obviously other assumptions are possible, some still more flexible than the mixture of two normals: for example, a mixture of three or more normals. Indeed, many other assumptions have been proposed, including variants in which a normal distribution is replaced by a distribution. These variants include the “Bayesian alphabet models” – so-called simply because they have been given names such as BayesA, BayesB, BayesC, etc. – that have been proposed for polygenic modeling, particularly breeding value prediction in genomic selection studies. Table 1 summarizes these models, and some other effect size distributions that have been proposed, together with relevant references (see also [53] and the references there in). Among these, the models most closely related to ours are BayesC [34] and BayesR [35]. Specifically, BayesC without a random effect is BVSR, and with a random effect is BSLMM (which we define below). BayesR models effect sizes using a mixture of three normal components plus a point mass at zero, although the relative variance for each normal distribution is fixed. 10.1371/journal.pgen.1003264.t001 Table 1 Summary of some effect size distributions that have been proposed for polygenic modeling. Effect Size Distribution Keywords Selected References Name Formula t BayesA [27], [32], [33], [40] point-t BayesB, BayesD, BayesD [27], [32]–[34], [40] t mixture BayesC [32], [33] point-normal BayesC, BayesC , BVSR [18], [19], [34] double exponential Bayesian Lasso [28], [39], [68] point-normal mixture BayesR [35] normal LMM, BLUP, Ridge Regression [22], [26], [28], [48] normal-exponential-gamma NEG [16] normal mixture BSLMM Present Work The reference list contains only a selection of relevant publications. Abbreviations: DE denotes double exponential distribution, NEG denotes normal exponential gamma distribution, and other abbreviations can be found in the main text. In the scaled t-distribution, and are the degree of freedom parameter and scale parameter, respectively. In the DE distribution, is the scale parameter. In the NEG distribution, and are the shape and scale parameters, respectively. Notes: 1. Some applications of these methods combine a particular effect size distribution with a random effects term, with covariance matrix , to capture sample structure or relatedness. If then this is equivalent to adding a normal distribution to the effect size distribution. The listed effect size distributions in this table do not include this additional normal component. 2. BayesC has been used to refer to models with different effect size distributions in different papers. 3. In some papers, keywords listed here have been used to refer to fitting techniques rather than effect size distributions. Given the wide range of assumptions for effect size distributions that have been proposed, it is natural to wonder which are the most appropriate for general use. However, answering this question is complicated by the fact that even given the effect size distribution there are a number of different ways that these models can be implemented in practice, both in terms of statistical issues, such as treatment of the hyper-parameters, and in terms of computational and algorithmic issues. Both these types of issues can greatly affect practical performance. For example, many approaches fix the hyper-parameters to specific values [27], [32], [33], [40] which makes them less flexible [34], [54]. Thus, in this paper we focus on a particular effect size distribution (5), which while not the most flexible among all that could be considered, is certainly more flexible than the one that has been most used in practice for estimating PVE (LMM), and admits certain computational methods that could not be applied in all cases. We consider in detail how to apply this model in practice, and the resulting advantages over LMM and BVSR (although we also compare with some other existing approaches). A key contribution of this paper is to provide new approaches to address two important practical issues: the statistical issue of how to deal with the unknown hyper-parameters , and the computational issue of how to fit the model. Notably, with the computational tools we use here, fitting the model (5) becomes, for a typical dataset, less computationally intensive than fitting BVSR, as well as providing gains in performance. With this background, we now turn to detailed description of the model, its prior specification and its computation algorithm. The Bayesian Sparse Linear Mixed Model In this paper we focus on the simple linear model (1) with mixture prior (5) on the effects. However, the computational and statistical methods we use here also apply to a more general model, which we refer to as the Bayesian Sparse Linear Mixed Model (BSLMM), and which includes the model (1) with (5) as a special case. The BSLMM consists of a standard linear mixed model, with one random effect term, and with sparsity inducing priors on the regression coefficients: (6) (7) (8) (9) where is an -vector of random effects with known covariance matrix . In referring to as the “random effects” we are following standard terminology from LMMs. Standard terminology also refers to the coefficients as “fixed effects”, but this phrase has a range of potential meanings [55] and so we avoid it here. Instead we use the term “sparse effects” for these parameters to emphasize the sparsity-inducing prior. It is straightforward to show that when , BSLMM is equivalent to the simple linear model (1) with mixture prior (5) on the effects. However, our discussion of prior specification, computational algorithms, and software, all apply for any . When we say that (6) is equivalent to (1) with (5), this equivalence refers to the implied probability model for given and the hyper-parameters . However, and are not equivalent (explaining our use of two different symbols): in (6) the random effect captures the combined small effects of all markers, whereas in (1) these small effects are included in . Since both our applications focus on the relationship between and , and not on interpreting estimates of or , we do not concern ourselves any further with this issue, although it may need consideration in applications where individual estimated genetic effects are of more direct interest (e.g. genetic association mapping). A related issue is the interpretation of the random effect in BSLMM: from the way we have presented the material is most naturally interpreted as representing a polygenic component, specifically the combined effect of a large number of small effects across all measured markers. However, if there are environmental factors that influence the phenotype and are correlated with genotype (e.g. due to population structure), then these would certainly affect estimates of , and consequently also affect estimates of other quantities, including the PVE. In addition, phenotype predictions from BSLMM will include a component due to unmeasured environmental factors that are correlated with measured genotypes. These issues are, of course, not unique to BSLMM – indeed, they apply equally to the LMM; see [56] and the response from [57] for relevant discussion. Finally, given the observation that a mixture of two normals is more flexible than a point-normal, it might seem natural to consider modifying (6) by making the assumption that comes from a mixture of two normal distributions rather than a point-normal. However, if then this modification is simply equivalent to changing the values of . Prior Specification The BSLMM involves (hyper-)parameters, , and . Before considering prior specification for these parameters, we summarize their interpretations as follows: and control the phenotype mean and residual variance. controls the proportion of values in (6) that are non-zero. controls the expected magnitude of the (non-zero) . controls the expected magnitude of the random effects . Appropriate values for these parameters will clearly vary for different datasets, so it seems desirable to estimate them from the data. Here we accomplish this in a Bayesian framework by specifying prior distributions for the parameters, and using Markov chain Monte Carlo (MCMC) to obtain approximate samples from their posterior distribution given the observed data. Although one could imagine instead using maximum likelihood to estimate the parameters, the Bayesian framework has several advantages here: for example, it allows for incorporation of external information (e.g. that most genetic markers will, individually, have small effects), and it takes into account of uncertainty in parameter estimates when making other inferences (e.g. phenotype prediction). For the mean and the inverse of error variance, , we use the standard conjugate prior distributions: (10) (11) where and denote, respectively, shape and rate parameters of a Gamma distribution. Specifically we consider the posterior that arises in the limits , and . These limits correspond to improper priors, but the resulting posteriors are proper, and scale appropriately with shifting or scaling of the phenotype vector [58]. In particular, these priors have the property that conclusions will be unaffected by changing the units of measurement of the phenotype, which seems desirable for a method intended for general application. Prior specification for the remaining hyper-parameters is perhaps more important. Our approach is to extend the prior distributions for BVSR described in [19]. Following [19] we place a uniform prior on : (12) where is total number of markers being analyzed. The upper and lower limit of this prior were chosen so that (the expected proportion of markers with non-zero ) ranges from to . A uniform prior on reflects the fact that uncertainty in in a typical GWAS will span orders of magnitude. A common alternative (see e.g. [18], [34]) is a uniform distribution on , but as noted in [19] this puts large weight on large numbers of markers having non-zero (e.g. it would correspond to placing 50% prior probability to the event that more than half of the markers have non-zero , and correspond to placing 90% prior probability to the event that more than 10% of the markers have non-zero ). To specify priors for and , we exploit the following idea from [19]: prior specification is easier if we first re-parameterize the model in terms of more interpretable quantities. Specifically we extend ideas from [19] to re-parameterize the model in terms of the (expected) proportion of phenotypic variance explained by the sparse effects and by the random effects. To this end, we define PVE (the total proportion of variance in phenotype explained by the sparse effects and random effects terms together) and PGE (the proportion of genetic variance explained by the sparse effects terms) as functions of , and : (13) (14) where the function V(x) is defined as (15) These definitions ensure that both PVE and PGE must lie in the interval . PVE reflects how well one could predict phenotype from the available SNPs if one knew the optimal as well as the random effects ; together with PVE, PGE reflects how well one could predict phenotype using alone. Since PVE and PGE are functions of , whose distributions depend on hyper-parameters , the prior distribution for PVE and PGE depends on the priors assigned to these hyper-parameters. In brief, our aim is to choose priors for the two hyper-parameters and so that the induced priors on both PVE and PGE are roughly uniform on 0 and 1. (Other distributions could be chosen if desired, but we consider this uniform distribution one reasonable default.) However, because the relationship between the distribution of PVE, PGE and the hyper-parameters is not simple, we have to make some approximations. Specifically, we introduce as approximations (they are ratios of expectations rather than expectations of ratios) to the expectations of PVE and PGE, respectively: (16) (17) where is the average variance of genotypes across markers, and is the mean of diagonal elements in . In other words, and , where and are the th elements of matrices and , respectively. See Text S1 for derivations. Intuitively, the term captures the expected genetic variance contributed by the sparse effects term (relative to the error variance), because is the expected number of causal markers, is the expected effect size variance of each causal marker (relative to the error variance), and is the average variance of marker genotypes. Similarly, the term captures the expected genetic variance contributed by the random effects term (relative to the error variance), because is the expected variance of the random effects (relative to the error variance) when the relatedness matrix has unit diagonal elements, while properly scales it when not. The parameter provides a natural bridge between the LMM and BVSR: when BSLMM becomes the LMM, and when BSLMM becomes BVSR. In practice, when the data favors the LMM, the posterior distribution of would mass near 0, and when the data favors BVSR, the posterior distribution of would mass near 1. In summary, the above re-parameterizes the model in terms of instead of . Now, instead of specifying prior distributions for , we rather specify prior distributions for . Specifically we use uniform prior distributions for : (18) (19) independent of one another and of . Since and approximate PVE and PGE, these prior distributions should lead to reasonably uniform prior distributions for PVE and PGE, which we view as reasonable defaults for general use. (If one had specific information about PVE and PGE in a given application then this could be incorporated here.) In contrast it seems much harder to directly specify reasonable default priors for (although these priors on do of course imply priors for ; see Text S1). Note that we treat and as approximations to PVE and PGE only for prior specification; when estimating PVE and PGE from data we do so directly using their definitions (13) and (14) (see below for details). Posterior Sampling Scheme To facilitate computation, we use the widely-used approach from [52] of introducing a vector of binary indicators that indicates whether the corresponding coefficients are non-zero. The point-normal priors for can then be written (20) (21) (22) where denotes the sub-vector of corresponding to the entries ; denotes the sub-vector of corresponding to the other entries, ; and denotes the number of non-zero entries in . We use MCMC to obtain posterior samples of ( ) on the product space , which is given by (23) The marginal likelihood can be computed analytically integrating out ; see below for further details. We use a Metropolis-Hastings algorithm to draw posterior samples from the above marginal distribution. In particular, we use a rank based proposal distribution for [19], which focus more of the computational time on examining SNPs with stronger marginal associations. We use the resulting sample from the posterior distribution (23) to estimate PVE and PGE as follows. For each sampled value of , we sample a corresponding value for from the conditional distribution . We then use each sampled value of to compute a sampled value of PVE and PGE, using equations (13) and (14). We estimate the posterior mean and standard deviation of PVE, PGE, from these samples. The novel part of our algorithm is a new efficient approach to evaluating the likelihood that considerably reduces the overall computational burden of the algorithm. The direct naive approach to evaluating this likelihood involves a matrix inversion and a matrix determinant calculation that scale cubically with the number of individuals , and this cost is incurred every iteration as hyper parameter values change. Consequently, this approach is impractical for typical association studies with large , and ad hoc approximations are commonly used to reduce the burden. For example, both [37] and [41] fix to some pre-estimated value. As we show later, this kind of approximation can reduce the accuracy of predicted phenotypes. Here, we avoid such approximations by exploiting recently developed computational tricks for LMMs [8], [9]. The key idea is to perform a single eigen-decomposition and use the resulting unitary matrix (consisting of all eigen vectors) to transform both phenotypes and genotypes to make the transformed values follow independent normal distributions. By extending these tricks to BSLMM we evaluate the necessary likelihoods much more efficiently. Specifically, after a single operation at the start of the algorithm, the per iteration computational burden is linear in (the same as BVSR), allowing large studies to be analyzed. Full details of the sampling algorithm appear in Text S2. URLs Software implementing our methods is included in the GEMMA software package, which is freely available at http://stephenslab.uchicago.edu/software.html. Results Simulations: PVE Estimation Both the LMM and BVSR have been used to estimate the PVE [19], [22]. Since the LMM assumes that all SNPs have an effect, while BVSR assumes that only a small proportion of SNPs have an effect, we hypothesize that BVSR will perform better when the true underlying genetic structure is sparse and LMM will perform better when the true genetic structure is highly polygenic. Further, because BSLMM includes both as special cases, we hypothesize that BSLMM will perform well in either scenario. To test these hypotheses, we perform a simulation using real genotypes at about 300,000 SNPs in 3,925 Australian individuals [22], and simulate phenotypes under two different scenarios. In Scenario I we simulate a fixed number of causal SNPs (with ), with effect sizes coming from a standard normal distribution. These simulations span a range of genetic architectures, from very sparse to highly polygenic. In Scenario II we simulate two groups of causal SNPs, the first group containing a small number of SNPs of moderate effect ( or ), plus a second larger group of SNPs of small effect representing a “polygenic component”. This scenario might be considered more realistic, containing a mix of small and larger effects. For both scenarios we added normally-distributed errors to phenotype to create datasets with true PVE = 0.6 and 0.2 (equation 13). We simulate 20 replicates in each case, and run the algorithms with all SNPs, including the simulated causal variants, so that the true PVE for typed markers is either 0.6 or 0.2 (if we excluded the causal variants then the true PVE would be unknown). Figure 1A and 1C, show the root of mean square error (RMSE) of the PVE estimates obtained by each method, and Figure 1B and 1D summarize the corresponding distributions of PVE estimates. In agreement with our original hypotheses, BVSR performs best (lowest RMSE) when the true model is sparse (e.g. Scenario I, or in Figure 1A, 1C). However, it performs very poorly under all the other, more polygenic, models. This is due to a strong downward bias in its PVE estimates (Figure 1B, 1D). Conversely, under the same scenarios, LMM is the least accurate method. This is because the LMM estimates have much larger variance than the other methods under these scenarios (Figure 1B,1D), although, interestingly, LMM is approximately unbiased even in these settings where its modeling assumptions are badly wrong. As hypothesized, BSLMM is robust across a wider range of settings than the other methods: its performance lies between LMM and BVSR when the true model is sparse, and provides similar accuracy to LMM when not. 10.1371/journal.pgen.1003264.g001 Figure 1 Comparison of PVE estimates from LMM (blue), BVSR (red), and BSLMM (purple) in two simulation scenarios. The x-axis show the number of causal SNPs (Scenario I) or the number of medium/small effect SNPs (Scenario II). Results are based on 20 replicates in each case. (A) (true PVE = 0.2) and (C) (true PVE = 0.6) show RMSE of PVE estimates. (B) (true PVE = 0.2) and (D) (true PVE = 0.6) show boxplots of PVE estimates, where the true PVE is shown as a horizontal line. Notice a break point on the y-axis in (C). Of course, in practice, one does not know in advance the correct genetic architecture. This makes the stable performance of BSLMM across a range of settings very appealing. Due to the poor performance of BVSR under highly polygenic models, we would not now recommend it for estimating PVE in general, despite its good performance when its assumptions are met. Simulations: Phenotype Prediction We also compare the three methods on their ability to predict phenotypes from genotypes, using the same simulations. To measure prediction performance, we use relative prediction gain (RPG; see Text S1). In brief, RPG is a standardized version of mean square error: RPG = 1 when accuracy is as good as possible given the simulation setup, and RPG = 0 when accuracy is the same as simply predicting everyone to have the mean phenotype value. RPG can be negative if accuracy is even worse than that. Figure 2 compares RPG of different methods for simulations with PVE = 0.6 (results for PVE = 0.2 are qualitatively similar, not shown). Interestingly, for phenotype prediction, the relative performance of the methods differs from results for PVE estimation. In particular, LMM performs poorly compared with the other two methods in all situations, except for Scenario I with , the Scenario that comes closest to matching the underlying assumptions of LMM. As we expect, BSLMM performs similarly to BVSR in scenarios involving smaller numbers of causal SNPs (up to in Scenario I), and outperforms it in more polygenic scenarios involving large numbers of SNPs of small effect (e.g. Scenario II). This is presumably due to the random effect in BSLMM that captures the polygenic component, or, equivalently, due to the mixture of two normal distributions in BSLMM that better captures the actual distribution of effect sizes. The same qualitative patterns hold when we redo these simulation comparisons excluding the causal SNPs (Figure S1) or use correlation instead of RPG to assess performance (Figure S2 and Figure S3). 10.1371/journal.pgen.1003264.g002 Figure 2 Comparison of prediction performance of LMM (blue), BVSR (red), and BSLMM (purple) in two simulation scenarios, where all causal SNPs are included in the data. Performance is measured by Relative Predictive Gain (RPG). True PVE = 0.6. Means and standard deviations (error bars) are based on 20 replicates. The x-axis show the number of causal SNPs (Scenario I) or the number of medium/small effect SNPs (Scenario II). For a potential explanation why LMM performs much less well for phenotype prediction than for PVE estimation, we note the difference between these two problems: to accurately estimate PVE it suffices to estimate the “average” effect size reliably, whereas accurate phenotype prediction requires accurate estimates of individual effect sizes. In situations where the normal assumption on effect sizes is poor, LMM tends to considerably underestimate the number of large effects, and overestimate the number of small effects. These factors can cancel one another out in PVE estimation, but both tend to reduce accuracy of phenotype prediction. Estimating PVE in Complex Human Traits To obtain further insights into differences between LMM, BVSR and BSLMMM, we apply all three methods to estimate the PVE for five traits in two human GWAS datasets. The first dataset contains height measurements of 3,925 Australian individuals with about 300,000 typed SNPs. The second dataset contains four blood lipid measurements, including high-density lipoprotein (HDL), low-density lipoprotein (LDL), total cholesterol (TC) and triglycerides (TG) from 1,868 Caucasian individuals with about 550,000 SNPs. The narrow sense heritability for height is estimated to be 0.8 from twin-studies [22], [59]. The narrow sense heritabilities for the lipid traits have been estimated, in isolated founder populations, to be 0.63 for HDL, 0.50 for LDL, 0.37 for TG in Hutterites [60], and 0.49 for HDL, 0.42 for LDL, 0.42 for TC and 0.32 for TG in Sardinians [61]. Table 2 shows PVE estimates from the three methods for the five traits. PVE estimates from BVSR are consistently much smaller than those obtained by LMM and BSLMM, which are almost identical for two traits and similar for the others. Estimates of PVE from both LMM and BSLMM explain over 50% of the narrow sense heritability of the five traits, suggesting that a sizable proportion of heritability of these traits can be explained, either directly or indirectly, by available SNPs. 10.1371/journal.pgen.1003264.t002 Table 2 PVE and PGE estimates for five human traits. Method Height HDL LDL TC TG PVE LMM 0.42 (0.08) 0.38 (0.15) 0.22 (0.18) 0.22 (0.17) 0.34 (0.17) BVSR 0.15 (0.03) 0.06 (0.01) 0.10 (0.08) 0.15 (0.07) 0.05 (0.06) BSLMM 0.41 (0.08) 0.34 (0.14) 0.22 (0.14) 0.26 (0.14) 0.29 (0.17) PGE BSLMM 0.12 (0.13) 0.21 (0.14) 0.27 (0.26) 0.46 (0.30) 0.18 (0.20) PVE estimates are obtained using LMM, BVSR and BSLMM, while PGE estimates are obtained using BSLMM. Values in parentheses are standard error (for LMM) or standard deviation of posterior samples (for BVSR and BSLMM). for height, and for other four traits. These results, with LMM and BSLMM providing similar estimates of PVE, and estimates from BVSR being substantially lower, are consistent with simulation results for a trait with substantial polygenic component. One feature of BSLMM, not possessed by the other two methods, is that it can be used to attempt to quantify the relative contribution of a polygenic component, through estimation of PGE, which is the proportion of total genetic variance explained by “large” effect size SNPs (or more precisely, by the additional effects of those SNPs above a polygenic background). Since the PGE is defined within an inevitably over-simplistic model, specifically that effect sizes come from a mixture of two normal distributions, and also because it will be influenced by unmeasured environmental factors that correlate with genetic factors, we caution against over-interpreting the estimated values. We also note that estimates of PGE for these data (Table 2) are generally not very precise (high posterior standard deviation). Nonetheless, it is interesting that the estimated PGE for height, at 0.12, is lower than for any of the lipid traits (ranging from 0.18 for TG to 0.46 for TC), and that all these estimates suggest a substantial contribution from small polygenic effects in all five traits. Predicting Disease Risk in the WTCCC Dataset To assess predictive performance on real data, we turn to the Wellcome trust case control consortium (WTCCC) 1 study [62], which have been previously used for assessing risk prediction [63]–[65]. These data include about 14,000 cases from seven common diseases and about 3,000 shared controls, typed at a total of about 450,000 SNPs. The seven common diseases are bipolar disorder (BD), coronary artery disease (CAD), Crohn's disease (CD), hypertension (HT), rheumatoid arthritis (RA), type 1 diabetes (T1D) and type 2 diabetes (T2D). We compared the prediction performance of LMM, BVSR and BSLMM for all seven diseases. Following [64], we randomly split the data for each disease into a training set (80% of individuals) and a test set (remaining 20%), performing 20 such splits for each disease. We estimated parameters from the training set by treating the binary case control labels as quantitative traits, as in [5], [9]. [This approach can be justified by recognizing the linear model as a first order Taylor approximation to a generalized linear model; we discuss directly modeling binary phenotypes in the Discussion section.] We assess prediction performance in the test set by area under the curve (AUC) [66]. Figure 3 shows AUC for the three methods on all seven diseases. As in our simulations, we find BSLMM performs as well as or better than either of the other two methods for all seven diseases. Indeed, the performance of BSLMM appears to compare favorably with previous methods applied to the same dataset [63]–[65] (a precise comparison with previous results is difficult, as some studies use slightly different splitting strategies [63], [65] and some do not perform full cross validation [64]). As might be expected from the simulation results, BVSR performs better than LMM in diseases where a small number of relatively strong associations were identified in the original study [62] (CD, RA and T1D) and worse in the others. We obtained qualitatively similar results when we measured performance using the Brier score instead of AUC (Text S3; Figure S4). 10.1371/journal.pgen.1003264.g003 Figure 3 Comparison of prediction performance of LMM (blue), BVSR (red), and BSLMM (purple) for seven diseases in the WTCCC dataset. Performance is measured by area under the curve (AUC), where a higher value indicates better performance. The order of the diseases is based on the performance of BSLMM. The mean and standard deviation of AUC scores for BSLMM in the seven diseases are 0.60 (0.02) for HT, 0.60 (0.03) for CAD, 0.61 (0.03) for T2D, 0.65 (0.02) for BD, 0.68 (0.02) for CD, 0.72 (0.01) for RA, 0.88 (0.01) for T1D. Finally, we caution that, although BSLMM performs well here relative to other methods, at the present time, for these diseases, its prediction accuracy is unlikely to be of practical use in human clinical settings. In particular, in these simulations the number of cases and controls in the test set is roughly equal, which represents a much easier problem than clinical settings where disease prevalence is generally low even for common diseases (see [64] for a relevant discussion). Predicting Quantitative Phenotypes in Heterogeneous Stock Mice In addition to the WTCCC dataset, we also assess perdition performance using a mouse dataset [67], which has been widely used to compare various phenotype prediction methods [37]–[39]. The mouse dataset is substantially smaller than the human data ( , with exact numbers varying slightly depending on the phenotype and the split). This makes it computationally feasible to compare with a wider range of other methods. Therefore, we include in our comparisons here five other related approaches, some of which have been proposed previously for phenotype prediction. Specifically we compare with: LMM-Bayes, a Bayesian version of the LMM, which we fit by setting in BSLMM using our software. Bayesian Lasso [39], [68], implemented in the R package BLR [39]. BayesA-Flex, our own modification of BayesA, which assumes a distribution for the effect sizes. Our modification involves estimating the scale parameter associated with the distribution from the data (Text S1). Although the original BayesA performs poorly in this dataset [38], this simple modification greatly improves its prediction performance (emphasizing again the general importance of estimating hyper-parameters from the data rather than fixing them to arbitrary values). We modified the R package BLR [39] to obtain posterior samples from this model. BayesC , implemented in the online software GenSel [34]. This implementation does not allow random effects, and therefore uses the same model as our BVSR, although with different prior distributions. BSLMM-EB (where EB stands for empirical Bayes; this is a slight abuse of terminology, since in this method the estimated hyper parameters are obtained under the model with ), an approximation method to fit BSLMM. The method fixes the variance component to its REML (restricted maximum likelihood) estimate obtained with , which is one of several strategies used in previous studies to alleviate the computational burden of fitting models similar to BSLMM [37], [41]. We sample posteriors from this model using our software. See Text S1 for further details. Following previous studies that have used these data for prediction [37]–[39] we focused on three quantitative phenotypes: CD8, MCH and BMI. These phenotypes have very different estimated narrow sense heritabilities: 0.89, 0.48, and 0.13 respectively [69]. Table S1 lists estimates of some key quantities for the three traits – including PVE, PGE and – obtained from LMM, BVSR and BSLMM. All three methods agree well on the PVE estimates, suggesting that the data is informative enough to overwhelm differences in prior specification for PVE estimation. Following [37], [38], we divide the mouse dataset roughly half and half into a training set and a test set. As the mice come from 85 families, and individuals within a family are more closely related than individuals from different families, we also follow previous studies and use two different splits of the data: the intra-family split mixes all individuals together and randomly divides them into two sets of roughly equal size; the inter-family split randomly divides the 85 families into two sets, where each set contains roughly half of the individuals. We perform 20 replicates for each split of each phenotype. It is important to note that the intra-family split represents an easier setting for phenotype prediction, not only because individuals in the test set are more related genetically to those in the training set, but also because the individuals in the test set often share a similar environment with those in the training set (specifically, in the intra-family split, many individuals in the test set share a cage with individuals in the training set, but this is not the case in the inter-family split). We apply each method using genotypes only, without other covariates. We obtain effect size estimates in the training dataset, and assess prediction performance using these estimates in the test set by root of mean square error (RMSE), where the mean is across individuals in the test set. We contrast the performance of other methods to BSLMM by calculating the RMSE difference, where a positive number indicates worse performance than BSLMM. We perform 20 inter-family splits and 20 intra-family splits for each phenotype. Figure 4 summarizes the prediction accuracy, measured by RMSE, of each method compared against BSLMM. Measuring prediction performance by correlation gives similar results (Figure S5). For the low-heritability trait BMI, where no measured SNP has a large effect, all methods perform equally poorly. For both the more heritable traits, CD8 and MCH, BSLMM consistently outperformed all other methods, which seem to split into two groups: LMM, LMM-Bayes and Bayesian Lasso perform least well and similarly to one another on average; BVSR, BayesA-Flex, BayesC and BSLMM-EB perform better, and similarly to one another on average. A general trend here is that accuracy tends to increase as model assumptions improve in their ability to capture both larger genetic effects, and the combined “polygenic” contribution of smaller genetic effects (and possibly also confounding environmental effects correlating with genetic background). In particular, the distribution underlying BayesA-Flex, which has a long tail that could capture large effects, performs noticeably better than either the normal or double-exponential distributions for effect sizes underlying LMM and Bayesian Lasso. 10.1371/journal.pgen.1003264.g004 Figure 4 Comparison of prediction performance of several models with BSLMM for three traits in the heterogenous stock mouse dataset. Performance is measured by RMSE difference with respect to BSLMM, where a positive value indicates worse performance than BSLMM. The x-axis shows two different ways to split the data into a training set and a test set, each with 20 replicates. The mean RMSE of BSLMM for the six cases are 0.70, 0.80, 0.79, 0.90, 0.98 and 0.99, respectively. Comparisons of pairs of closely-related methods yield additional insights into factors that do and do not affect prediction accuracy. The fact that BSLMM performs better than BSLMM-EB illustrates how the approximation used in BSLMM-EB can degrade prediction accuracy, and thus demonstrates the practical benefits of our novel computational approach that avoids this approximation. Similarly, the superior performance of BayesA-Flex over BayesA (which performed poorly; not shown) also illustrates the benefits of estimating hyper parameters from the data, rather than fixing them to pre-specified values. The similar performance between BVSR and BayesC , which fit the same model but with different priors, suggests that, for these data, results are relatively robust to prior specification. Presumably, this is because the data are sufficiently informative to overwhelm the differences in prior. Computational Speed The average computational time taken for each method on the Mouse data is shown in Table 3. Some differences in computational time among methods may reflect implementational issues, including the language environment in which the methods are implemented, rather than fundamental differences between algorithms. In addition, computing times for many methods will be affected by the number of iterations used, and we did not undertake a comprehensive evaluation of how many iterations suffice for each algorithm. Nonetheless, the results indicate that our implementation of BSLMM is competitive in computing speed with the other (sampling-based) implementations considered here. 10.1371/journal.pgen.1003264.t003 Table 3 Mean computation time, in hours, of various methods for the mouse dataset. Method Time in hrs (sd) LMM 0.007 (0.002) LMM-Bayes 0.14 (0.02) BSLMM-EB 2.44 (3.52) BSLMM 3.86 (4.13) BVSR 9.20 (6.36) BayesC 39.4 (11.7) BayesA-Flex 68.6 (8.06) Bayesian Lasso 78.6 (23.4) Values in parentheses are standard deviations. Means and standard deviations are calculated based on 2.1 million MCMC iterations in 120 replicates: 20 intra-family and 20 inter-family splits for three phenotypes. Computations were performed on a single core of an Intel Xeon L5420 2.50 GHz CPU. Since computing times for many methods will vary with number of iterations used, and we did not undertake a comprehensive evaluation of how many iterations suffice for each algorithm, these results provide only a very rough guide to the relative computational burden of different methods. In particular, we note that BSLMM is computationally faster than BVSR. This is unexpected, since BSLMM is effectively BVSR plus a random effects term, and the addition of a random effects term usually complicates computation. The explanation for this is that the (per-iteration) computational complexity of both BSLMM and BVSR depends, quadratically, on the number of selected SNPs in the sparse effects term ( ), and this number can be substantially larger with BVSR than with BSLMM, because with BVSR additional SNPs are included to mimic the effect of the random effects term in BSLMM. The size of this effect will vary among datasets, but it can be substantial, particularly in cases where there are a large number of causal SNPs with small effects. To illustrate this, Table 4 compares mean computation time for BSLMM vs BVSR for all datasets used here. For simulated data with a small number of causal SNPs, BSLMM and BVSR have similar computational times. However, in other cases (e.g. PVE = 0.6, S = 10,000 in Scenario I) BSLMM can be over an order of magnitude faster than BVSR. In a sense, this speed improvement of BSLMM over BVSR is consistent with its hybrid nature: in highly polygenic traits, BSLMM tends to behave similarly to LMM, resulting in a considerable speed gain. 10.1371/journal.pgen.1003264.t004 Table 4 Mean computation time, in hours, of BVSR and BSLMM in all examples used in this study. Simulations PVE = 0.2, Number of Causal SNPs 10 100 1000 10000 10/10000 100/10000 BVSR 8.25 (1.11) 50.0 (17.3) 46.3 (25.0) 32.8 (25.0) 50.6 (23.9) 35.2 (24.7) BSLMM 8.44 (2.04) 16.9 (4.06) 5.44 (0.23) 5.19 (0.20) 29.3 (17.2) 37.5 (19.1) PVE = 0.6, Number of Causal SNPs 10 100 1000 10000 10/10000 100/10000 BVSR 7.43 (0.72) 36.9 (5.71) 118 (8.94) 96.1 (12.0) 75.4 (28.9) 92.8 (15.0) BSLMM 7.34 (1.05) 41.2 (5.12) 39.8 (15.0) 5.13 (0.34) 13.5 (5.52) 45.9 (16.6) Real Data Diseases BD CAD CD HT RA T1D T2D BVSR 131 (20.3) 110 (20.3) 105 (13.9) 114 (21.0) 12.4 (3.52) 14.8 (2.47) 123 (22.0) BSLMM 21.7 (13.6) 22.0 (16.2) 57.6 (24.6) 32.8 (23.8) 9.58 (1.17) 14.5 (2.52) 38.7 (20.3) Quantitative Traits Height HDL LDL TC TG CD8 MCH BMI BVSR 96.1 2.94 21.4 24.4 18.8 5.89 (1.87) 10.5(5.83) 11.2(8.30) BSLMM 77.4 3.35 7.24 24.0 6.53 1.14 (1.05) 2.45(3.13) 7.97(3.79) Computations were performed on a single core of an Intel Xeon L5420 2.50 GHz CPU, with 2.1 million MCMC iterations. Values in parentheses are standard deviations. Means and standard deviations are calculated based on 20 replicates in simulations, 20 replicates in the WTCCC dataset, and 40 replicates—20 intra-family and 20 inter-family splits—in the mouse dataset. Discussion We have presented novel statistical and computational methods for BSLMM, a hybrid approach for polygenic modeling for GWAS data that simultaneously allows for both a small number of individually large genetic effects, and combined effects of many small genetic effects, with the balance between the two being inferred from the data in hand. This hybrid approach is both computationally tractable for moderately large datasets (our implementation can handle at least 10,000 individuals with 500,000 SNPs on our moderately-equipped modern desktop computer), and is sufficiently flexible to perform well in a wide range of settings. In particular, depending on the genetic architecture, BSLMM is either as accurate, or more accurate, than the widely-used LMM for estimating PVE of quantitative traits. And for phenotype prediction BSLMM consistently outperformed a range of other approaches on the examples we considered here. By generalizing two widely-used models, and including both as special cases, BSLMM should have many applications beyond polygenic modeling. Indeed, despite its increased computational burden, we believe that BSLMM represents an attractive alternative to the widely-used LASSO [70] for general regression-based prediction problems. Although it was not our focus here, BSLMM can be easily modified to analyze binary phenotypes, including for example, a typical human case-control GWAS. For PVE estimation, one can directly apply BSLMM, treating the 1/0 case-control status as a quantitative outcome, and then apply a correction factor derived by [24] to transform this estimated PVE on the “observed scale” to an estimated PVE on a latent liability scale. This correction, for which we supply an alternative derivation in Text S3, corrects for both ascertainment and the binary nature of case-control data. For phenotype prediction, one can again directly apply BSLMM, treating the 1/0 case-control status as a quantitative outcome, as we do here for the WTCCC dataset, and interpret the resulting phenotype predictions as the estimated probability of being a case. Although in principle one might hope to improve on this by modifying BSLMM to directly model the binary outcomes, using a probit link for example, we have implemented this probit approach and found that not only is it substantially more computationally expensive (quadratic in instead of linear in ), but it performed slightly worse than treating the binary outcomes as quantitative, at least in experiments based on the mouse phenotypes considered here (Text S3 and Figure S6), which is consistent with previous findings in quantitative trait loci mapping [71]. This may partly reflect inaccuracies introduced by the known greater computational burden and corresponding mixing issues with probit models (e.g. [72]) which are magnified here by the polygenic nature of the traits, and partly reflect robustness of linear models to model misspecification. The computational innovations we introduce here, building on work by [8], [9], make BSLMM considerably more tractable than it would otherwise be. Nonetheless, the computational burden, as with other posterior sampling based methods, remains heavy, both due to memory requirements (e.g. to store all genotypes) and CPU time (e.g. for the large number of sampling iterations required for reasonable convergence). Although more substantial computational resources will somewhat increase the size of data that can be tackled, further methodological innovation will likely be required to apply BSLMM to the very large datasets that are currently being collected. In addition to providing a specific implementation that allows BSLMM to be fitted to moderately large datasets, we hope that our work also helps highlight some more general principles for improving polygenic modeling methodology. These include: The benefits of characterizing different methods by their effect size distribution assumptions. While this point may seem obvious, and is certainly not new (e.g. [40], [73]), polygenic modeling applications often focus on the algorithm used to fit the model, rather than the effect size distribution used. While computational issues are very important, and often interact with modeling assumptions, we believe it is important to distinguish, conceptually, between the two. One benefit of characterizing methods by their modeling assumptions is that it becomes easier to predict which methods will tend to do well in which settings. The importance of selecting a sufficiently flexible distribution for effect sizes. The version of BSLMM we focus on here (with ) assumes a mixture of two (zero-mean) normals for the effect size distribution. Our examples demonstrate the gain in performance this achieves compared to less flexible distributions such as a single normal (LMM) or a point-normal (BVSR). More generally, in our phenotype prediction experiments, methods with more flexible effect size distributions tended to perform better than those with less flexible distributions. The importance of estimating hyper-parameters from data, rather than fixing them to pre-specified values. Here we are echo-ing and reinforcing similar themes emphasized by [34] and [19]. Indeed, our comparison between BSLMM and BSLMM-EB for phenotype prediction illustrates the benefits not only of estimating hyper-parameters from the data, but of doing so in an integrated way, rather than as a two-step procedure. The attractiveness of specifying prior distributions for hyper-parameters by focusing on the proportion of variance in phenotypes explained by different genetic components (e.g. PVE and PGE in our notation). This idea is not limited to BSLMM, and could be helpful even with methods that make use of other effect size distributions. One question to which we do not know the answer is how often the mixture of two normal distributions underlying BSLMM will be sufficiently flexible to capture the actual effect size distribution, and to what extent more flexible distributional assumptions (e.g. a mixture of more than two normals, or a mixture of distributions with degrees of freedom estimated from the data) will produce meaningful gains in performance. It seems likely that, at least in some cases, use of a more flexible distribution will improve performance, and would therefore be preferable if it could be accomplished with reasonable computational expense. Unfortunately some of the tricks we use to accomplish computational gains here may be less effective, or difficult to apply, for more flexible distributions. In particular, the tricks we use from [8] and [9] may be difficult to extend to allow for mixtures with more than two components. In addition, for some choices of effect size distribution, one might have to perform MCMC sampling on the effect sizes directly, rather than sampling , integrating out analytically, as we do here. It is unclear whether this will necessarily result in a loss of computational efficiency: sampling reduces computational expense per update at the cost of increasing the number of updates necessary (sampling by integrating over analytically ensures faster mixing and convergence [74], [75]). Because of these issues, it is difficult to predict which effect size distributions will ultimately provide the best balance between modeling accuracy and computational burden. Nonetheless, compared with currently available alternatives, we believe that BSLMM strikes an appealing balance between flexibility, performance, and computational tractability. Supporting Information Figure S1 Comparison of prediction performance of LMM (blue), BVSR (red) and BSLMM (purple) in two simulation scenarios, where all causal SNPs are excluded from the data. Performance is measured by Relative Predictive Gain (RPG). True PVE = 0.6. Means and standard deviations (error bars) are based on 20 replicates. The x-axis show the number of causal SNPs (Scenario I) or the number of medium/small effect SNPs (Scenario II). (EPS) Click here for additional data file. Figure S2 Comparison of prediction performance of LMM (blue), BVSR (red) and BSLMM (purple) in two simulation scenarios, where all causal SNPs are included in the data. Performance is measured by correlation. True PVE = 0.6. Means and standard deviations (error bars) are based on 20 replicates. The x-axis show the number of causal SNPs (Scenario I) or the number of medium/small effect SNPs (Scenario II). (EPS) Click here for additional data file. Figure S3 Comparison of prediction performance of LMM (blue), BVSR (red) and BSLMM (purple) in two simulation scenarios, where all causal SNPs are excluded from the data. Performance is measured by correlation. True PVE = 0.6. Means and standard deviations (error bars) are based on 20 replicates. The x-axis show the number of causal SNPs (Scenario I) or the number of medium/small effect SNPs (Scenario II). (EPS) Click here for additional data file. Figure S4 Comparison of prediction performance of LMM (blue), BVSR (red) and BSLMM (purple) for seven diseases in the WTCCC dataset. Performance is measured by Brier score, where a lower score indicates better performance. The order of the diseases is based on the performance of BSLMM. The mean and standard deviation of Brier scores for BSLMM in the seven diseases are 0.232 (0.004) for HT, 0.230 (0.004) for CAD, 0.230 (0.003) for T2D, 0.222 (0.004) for BD, 0.211 (0.004) for CD, 0.204 (0.004) for RA, 0.139 (0.006) for T1D. (EPS) Click here for additional data file. Figure S5 Comparison of prediction performance of several models with BSLMM for three traits in the heterogenous stock mouse dataset. Performance is measured by correlation difference with respect to BSLMM, where a positive value indicates better performance than BSLMM. The x-axis shows two different ways to split the data into a training set and a test set, each with 20 replicates. The mean correlation of BSLMM for the six cases are 0.72, 0.61, 0.61, 0.47, 0.21 and 0.14, respectively. (EPS) Click here for additional data file. Figure S6 Comparison of prediction performance between BSLMM and probit BSLMM for three binary traits in the heterogenous stock mouse dataset. Performance is measured by Brier score difference with respect to BSLMM, where a positive value indicates worse performance than BSLMM. The x-axis shows two different ways to split the data into a training set and a test set, each with 20 replicates. The mean Brier scores of BSLMM for the six cases are 0.185, 0.205, 0.201, 0.236, 0.245 and 0.249, respectively. (EPS) Click here for additional data file. Table S1 Estimates of PVE, PGE and for CD8, MCH and BMI in the mouse dataset. PVE estimates are obtained using LMM, BVSR and BSLMM, estimates are obtained using BVSR and BSLMM, and PGE estimates are obtained using BSLMM. Values in parentheses are standard error (for LMM) or standard deviation of posterior samples (for BVSR and BSLMM). for CD8, for MCH, and for BMI. (PDF) Click here for additional data file. Text S1 Detailed Methods. (PDF) Click here for additional data file. Text S2 Detailed MCMC Strategy for BSLMM. (PDF) Click here for additional data file. Text S3 The Probit BSLMM and Binary Traits. (PDF) Click here for additional data file.
- Record: found
- Abstract: found
- Article: found
Web-Based Genome-Wide Association Study Identifies Two Novel Loci and a Substantial Genetic Component for Parkinson's Disease
Chuong B. Do, Joyce Tung, Elizabeth Dorfman … (2011)
Introduction To date, a number of different genetic susceptibility factors have been identified for Parkinson's disease. Autosomal dominant factors involved in PD include mutations in the SNCA ( -synuclein) [1], [2] and LRRK2 (leucine-rich repeat kinase 2) [3], [4] genes. Autosomal recessive factors include mutations in the PARK2 (parkin) [5], PINK1 (PTEN induced putative kinase 1) [6], PARK7 (DJ1) [7], and ATP13A2 (ATPase type 13A2) genes [8], [9]. Parkinson's disease is sometimes thought of as consisting of an early-onset form, characterized by familial clustering and high penetrance mutations, and a late-onset form, which occurs more sporadically. In contrast with the evidence for Mendelian inheritance of early-onset PD, studies comparing rates of concordance in monozygotic and dizygotic twins [10]–[12] have traditionally yielded low estimates of heritability for late-onset PD. Evidence of familial aggregation in late-onset PD, when present, is thus sometimes attributed to shared environmental effects or ascertainment bias (see [13], but cf., [14]). Nonetheless, genome-wide association studies have uncovered a few new genes involved in late-onset PD in European [15]–[19] and Japanese [20] populations. These studies have shown repeatedly that common variation in SNCA and an inversion of the region containing the MAPT (microtubule-associated protein tau) gene are associated with PD. In addition, NUCKS1 (nuclear casein kinase and cyclin-dependent kinase substrate 1) [16], [20], the HLA (human leukocyte antigen) region [18], GAK (cyclin G associated kinase) [15], [19], BST1 (bone marrow stromal cell antigen 1) [20], [21], and five additional loci [22] have recently been associated with PD. Here, we present a genome-wide association study of PD with a number of distinguishing features. The recruitment of PD cases took place primarily through targeted emails to PD foundations and support groups over the course of 18 months. The large set of controls was recruited through the 23andMe customer database. Determination of case status was conducted through a set of online questionnaires. We present three main scientific results. First, we identify two novel loci associated with PD and replicate many more. Second, we present lower-bound estimates of PD heritability based on observed genome-wide sharing that imply a large fraction of the genetic component underlying the etiology of PD has not yet been discovered. Third, we use sparse regression techniques to construct risk estimation algorithms that account for roughly 6–7% of the total variance in liability to PD and that suggest the existence of true associations lying just beyond genome-wide significance. Results Participants were drawn from the customer database of the personal genetics company, 23andMe, Inc. The majority of cases were recruited into that database through PD support groups and tertiary clinics. All cases reported via web-based surveys having been diagnosed with Parkinson's disease by a physician. Most cases (approximately 84%) also provided detailed information about their disease progression, other diagnoses, symptoms, response to medication, and family history. All participants included in this study were unrelated individuals of primarily European ancestry, based on the criteria described in Materials and Methods. We used two different sources of data for validating SNPs discovered and models constructed using the 23andMe cohort. To replicate our association results, we exchanged -values with the International Parkinson Disease Genomics Consortium (IPDGC), whose dataset consisted of 6,584 cases and 15,470 controls compiled from seven separate cohorts containing individuals of European descent [23]. To validate our risk prediction methods, we used data from the National Institute of Neurological Disease and Stroke (NINDS) Database (see Materials and Methods for details). We did not attempt to replicate our novel associations on the NINDS dataset due to lack of statistical power; similarly, we did not validate our risk prediction methods on the IPDGC cohort as we did not have access to the genetic data for this group. Summary statistics describing all three datasets are provided in Table 1. 10.1371/journal.pgen.1002141.t001 Table 1 Description of cohorts. Description Number Age % Male Age of onset 23andMe controls 29624 48.2 (16.0) 58.5% – 23andMe cases 3426 64.3 (10.6) 60.3% 57.4 (10.7) IPDGC controls 15470 – – – IPDGC cases 6584 – – – NINDS controls 799 58.6 (16.4) 41.9% – NINDS cases 932 66.2 (11.0) 59.8% 58.5 (13.1) Age is the average current age for the 23andMe cohort and the average age at collection for the NINDS cohort. Standard deviations are given in parentheses. Associations We performed a GWAS using the 23andMe dataset consisting of 3,426 cases and 29,624 controls, controlling for age, sex, genotyping platform, and five principal components. All 23andMe samples were genotyped using a custom Illumina HumanHap 550+ panel, with 522,782 markers passing quality control (see Materials and Methods). Manhattan and q-q plots can be found in Figures S1 and S2. All SNPs with -values under in the 23andMe cohort are shown in Table 2. Summary data for the SNPs in Table 2 can be found in Table S1. All SNPs with -values under can be found in Table S2. Using a cutoff of for significance based on a Bonferroni correction across all markers, we identified two novel regions–SCARB2 and SREBF1/RAI1–and replicated six previously reported regions–LRRK2, SNCA, GBA, MAPT, MCCC1/LAMP3, and GAK. A seventh replication (SLC41A1/PARK16) and two other potentially novel regions (RIT2/SYT4 and USP25) appear nearly genome-wide significant as well. 10.1371/journal.pgen.1002141.t002 Table 2 GWAS results for all SNPs with in the 23andMe cohort. SNP Chr Position Region Alleles MAF Cohort OR rs34637584 12 39020469 LRRK2 G/A 0.002 23andMe 9.615 (6.43–14.37) IPDGC – – i4000416 1 153472258 GBA T/C 0.005 23andMe 4.048 (3.08–5.32) IPDGC – – rs356220 4 90860363 SNCA C/T 0.375 23andMe 1.285 (1.22–1.36) IPDGC – – rs12185268 17 41279463 MAPT A/G 0.211 23andMe 0.769 (0.72–0.82) IPDGC – – rs10513789 3 184242767 MCCC1/LAMP3 T/G 0.201 23andMe 0.803 (0.75–0.86) IPDGC 0.873 (0.83–0.92) rs6812193 4 77418010 SCARB2 C/T 0.365 23andMe 0.839 (0.79–0.89) IPDGC 0.90 (0.86–0.94) rs6599389 4 929113 GAK G/A 0.075 23andMe 1.311 (1.19–1.44) IPDGC – – rs11868035 17 17655826 SREBF1/RAI1 G/A 0.309 23andMe 0.851 (0.80–0.90) IPDGC 0.95 (0.91–0.996) 0.033 rs823156 1 204031263 SLC41A1 A/G 0.183 23andMe 0.827 (0.77–0.89) IPDGC – – rs4130047 18 38932233 RIT2/SYT4 T/C 0.313 23andMe 1.161 (1.10–1.23) IPDGC 1.077 (1.03–1.13) 0.0014 rs2823357 21 15836776 USP25 G/A 0.376 23andMe 1.149 (1.09–1.21) IPDGC 0.971 (0.93–1.02) 0.187 All genomic positions are given with respect to NCBI build 36.3. Alleles are listed as major/minor and are specified for the forward strand. Odds ratios per copy of the minor allele and -values are provided for the 23andMe cohort and, where requested, the IPDGC replication set. Minor allele frequencies are provided for the 23andMe cohort. The first novel association is rs6812193, with an odds ratio (OR) of and -value of , in an intron of FAM47E (see Figure 1), upstream of SCARB2. This SNP replicates in the IPDGC cohort with an OR of and -value of . The second novel association is rs11868035, with an OR of and -value of , located in an intron of SREBF1 (see Figure 2). This association also replicates in the IPDGC cohort with an OR of and -value of 0.03. Of potential interest is a non-synonymous variant (proline to threonine change), with a -value of , in RAI1, rs11649804, in tight linkage disequilibrium (LD) with rs11868035 ( ). 10.1371/journal.pgen.1002141.g001 Figure 1 Plot of -values around rs6812193 and SCARB2. In the plot, circles represent unannotated SNPs, upside-down triangles represent non-synonymous variants, and boxes with an “x” are SNPs in regions that are highly conserved across 44 placental mammals. Colors depict the squared correlation ( ) of each SNP with the most associated SNP (i.e., rs6812193). Purple designates the SNP with the strongest association, and gray indicates SNPs for which information was missing. Plots were produced using the LocusZoom program [71]. 10.1371/journal.pgen.1002141.g002 Figure 2 Plot of -values around rs11868035 and SREBF1/RAI1. Colors depict the squared correlation ( ) of each SNP with rs11868035. For details, see Figure 1. Among replications of previously reported associations, rs34637584 is the non-synonymous G2019S mutation in the LRRK2 gene, well known to be associated with PD [24]. GBA N370S is one of the mutations causing Gaucher's disease and has recently been associated with PD [25], [26]. These two SNPs, both rare variants, were included as part of the custom set of variants used to genotype the 23andMe cohort. The associations with SNCA, MAPT, GAK, and SLC41A1 have been reported multiple times. Here we provide the first independent confirmation of the association of rs10513789 in the MCCC1/LAMP3 region with PD, as first reported in [22]. Of the three suggestive associations that do not reach genome-wide significance, rs823156 near SLC41A1/PARK16 has been previously reported [20]. The association with rs4130047 (in an intron of RIT2, with an OR of 1.16 and -value of ) is not quite significant, though it independently appears in the IPDGC cohort with a replication -value of , and also is included in the supplement of [15] as a suggestive association under a recessive model. The last suggestive SNP, rs2823357, lies 170 kb upstream of USP25, a ubiquitin-specific protease. This association, however, fails to replicate in the IPDGC cohort, with a -value of . See Figure 5 and Figure 6 in [15] for plots of the RIT2/SYT4 and USP25 regions. On the basis of candidate gene studies or modest significance levels in previous GWASs, researchers have proposed associations for many genes with PD to date. We used the set of “Top Results” from the meta-analysis at http://www.pdgene.org/ [27] as well as all SNPs appearing in a PD GWAS with -values under from [28]. After removing SNPs for which we did not have a good proxy, and omitting highly correlated or duplicate SNPs, we were left with 42 potential replications. In addition to LRRK2 G2019S, 19 other previously reported associations replicated with the correct directionality in the 23andMe cohort using a significance threshold of 0.05 (see Table 3). Of these, 17 of our confidence intervals include the published OR. Of the two that did not, one was using a proxy SNP with a rather weak of 0.16, so it is not surprising that our OR is weaker in this case. 10.1371/journal.pgen.1002141.t003 Table 3 Replication of previously reported associations. Published SNP (Proxy) Region Alleles 23andMe OR (CI) Pub. OR (CI) Pop Ref. Grade GBA N370S (i4000416) GBA T/C 4.048 (3.08–5.32) 3.28 (2.41–4.47) All [27] B rs356220 SNCA C/T 1.285 (1.22–1.36) 1.32 (1.26–1.38) All [27] A MAPT-H1H2 (rs1876828) MAPT C/T 0.764 (0.71–0.82) 0.76 (0.72–0.80) Euro [27] A rs6812193 SCARB2 C/T 0.839 (0.79–0.89) 0.89 (NR) Euro [16] – rs823156 SLC41A1 A/G 0.827 (0.77–0.89) 0.82 (0.75–0.89) Asian [27] A rs11711441 (rs11716740) LAMP3 C/T 0.821 (0.76–0.89) 0.82 (0.74–0.90) Euro [22] – rs11248060 GAK C/T 1.202 (1.11–1.30) 1.24 (1.10–1.40) All [27] C rs2102808 (rs9917256) STK39 G/A 1.199 (1.11–1.30) 1.28 (1.20–1.36) Euro [22] – rs4698412 BST1 A/G 0.891 (0.84–0.94) 0.87 (0.82–0.91) Asian [27] A rs1491942 (rs11175655) LRRK2 G/A 0.00016 1.167 (1.08–1.26) 1.19 (1.13–1.25) Asian [22] – rs823128 NUCKS1 A/G 0.00019 0.758 (0.65–0.88) 0.70 (0.64–0.76) Asian [27] A chr1:154105678 (rs10737170) SYT11 A/C 0.00047 1.165 (1.07–1.27) 1.67 (1.50–1.84) Euro [22] – rs12817488 (rs11060112) CCDC62 A/C 0.0072 0.920 (0.86–0.98) 0.86 (0.82–0.91) Euro [22] – rs2282048 (rs872606) FARP1 A/C 0.0097 0.932 (0.88–0.98) 0.91 (0.84–0.99) All [27] C rs12718379 FGF20 A/G 0.011 1.072 (1.02–1.13) 1.09 (1.01–1.18) All [27] C rs7077361 ITGA8 T/C 0.0114 0.900 (0.83–0.98) 0.84 (NR) Euro [16] – rs10200894 2q36.3 C/G 0.0136 0.889 (0.81–0.98) 0.92 (0.83–1.01) Euro [27] C rs3129882 HLA A/G 0.0194 1.066 (1.01–1.13) 1.16 (1.02–1.32) All [27] C rs4880 SOD2 A/G 0.0304 0.943 (0.89–0.99) 0.88 (0.74–1.04) Asian [27] B rs797906 GLIS1 C/A 0.0578 1.055 (1.00–1.11) 1.08 (1.01–1.15) All [27] C rs7617877 3p24.1 G/A 0.0859 1.050 (0.99–1.11) 1.23 (1.13–1.33) Euro [19] – rs6280 DRD3 T/C 0.129 0.957 (0.90–1.01) 1.08 (1.02–1.15) All [27] C rs1079597 DRD2 C/T 0.157 1.056 (0.98–1.14) 1.17 (1.00–1.36) All [27] C rs6710823 (rs4954218) AMCSD T/G 0.194 1.042 (0.98–1.11) 1.38 (1.29–1.47) Euro [22] – rs17115100 CYP17A1 G/T 0.198 1.061 (0.97–1.16) 0.80 (NR) Euro [16] – rs7412 APOE C/T 0.2 1.067 (0.97–1.18) 1.15 (1.03–1.28) All [27] C rs12063142 TAS1R2 C/T 0.252 1.035 (0.98–1.10) NR (NR) Euro [17] – rs2010795 PDXK G/A 0.277 1.032 (0.98–1.09) 1.09 (1.02–1.16) All [27] C rs10464059 (rs1862326) 5q35.3 G/T 0.308 0.962 (0.89–1.04) 1.33 (1.19–1.52) Euro [17] – rs1799836 MAOB T/C 0.414 0.983 (0.94–1.03) 1.10 (1.01–1.20) All [27] C rs11030104 BDNF A/G 0.485 0.977 (0.92–1.04) 1.12 (1.04–1.22) All [27] C rs1043424 PINK1 A/C 0.492 1.021 (0.96–1.08) 0.91 (0.81–1.01) Euro [27] C rs1994090 LRRK2 T/G 0.496 1.023 (0.96–1.09) 1.39 (1.24–1.56) Asian [20] – rs1801133 MTHFR G/A 0.506 0.981 (0.93–1.04) 1.12 (1.02–1.22) Asian [27] B rs1223271 C20orf82 G/A 0.553 0.976 (0.90–1.06) 0.85 (NR) Euro [16] – rs17329669 7p14.2 A/G 0.56 0.978 (0.91–1.05) 1.13 (1.03–1.24) All [27] C rs12431733 BMP4 C/T 0.678 0.989 (0.94–1.04) 1.13 (NR) Euro [16] – rs5174 LRP8 C/T 0.841 0.994 (0.94–1.05) 0.93 (0.87–1.00) All [27] C rs13312 USP24 C/G 0.874 0.995 (0.93–1.06) 0.76 (0.66–0.86) All [27] A rs1801582 PARK2 C/G 0.881 0.995 (0.93–1.07) 0.79 (0.64–0.97) All [27] C rs1805874 (rs2205108) CALB1 G/T 0.882 1.004 (0.95–1.06) 1.12 (1.01–1.25) All [27] C rs4837628 DBC1 T/C 0.925 0.997 (0.95–1.05) 0.79 (0.72–0.87) Euro [17] – SNPs were taken from the PDGene “Top Results” list of meta-analyses [27] and the NHGRI list of associations [57]. Alleles are given with respect to the forward genomic strand for NCBI build 36.3 and are listed as major/minor. Where a proxy SNP was used, alleles refer to the proxy SNP. Published OR is the published odds ratio per copy of the minor allele for the association, as reported in the corresponding reference. Overall grades for SNPs based on the Venice criteria [72] were taken from the PDGene list, where available, and omitted otherwise. “NR” means that an OR or CI was not reported. -values and power calculations were calculated assuming a two-sided test. Our power to replicate a given association conditional on the published odds ratio and the minor allele frequency using a 0.05 threshold for significance was above 86% for all associations except for rs10200894, for which it was 59%. “Pop” refers to the ancestry in which the association was discovered, as taken from the PDGene list or the original paper where applicable. “All” indicates that multiple studies were used in the PDGene meta-analysis, irrespective of ancestry. We had good power (over 86% in all but one case) to replicate all 42 of these associations, assuming the reported odds ratio (from the meta-analysis in the case of associations from [27], from the original paper otherwise) was correct. Thus the failure to replicate many of the reported associations (including two with “A” or “B” meta-analysis grades) is likely partially due to inflation of the odds ratios in those reports, although a few of the associations that were discovered in Asian populations, such as rs1994090, may simply not have the same effect in European populations. Finally, we note that in all analyses above, we restricted consideration to a log-additive model of association. Allowance for dominant and recessive models might lead to increased power for detection in cases where a log-additive model is not appropriate, and may also affect the success rates in our replication experiment. Heritability To characterize the extent to which genetic factors tagged on genotyping panels play a role in PD susceptibility, we applied a recently proposed approach for estimating heritability based on genome-wide sharing between distantly related individuals [29], [30]. Using the 23andMe cohort, we estimated the heritability of PD to be 0.272 with 95% CI of 0.229 to 0.315. This estimate refers only to the proportion of phenotypic variance arising from causal variants that are in LD with the SNPs on our genotyping platform, which may be less than the corresponding proportion for all causal variants. This estimate has only a mild dependence on the assumed prevalence: using prevalences of or gives estimates of or , respectively. Thus, our estimates generally suggest a lower-bound on the actual heritability in the 0.25 to 0.3 range. Table 4 compares our heritability estimates using the 23andMe cohort with an estimate computed for the NINDS cohort based on the same analytic methods, and with numbers obtained from the literature. Where only relative recurrence risk ratios were provided, we inferred the corresponding heritability of liability under an assumption of no shared environmental covariance [31]; in practice, such an assumption is unlikely to hold for close relatives, and as such, the estimates of heritability we have inferred from those studies are likely to be upwardly biased. We note that our estimates of heritability for PD are most consistent with estimates from prior twin studies, though with substantially tighter confidence intervals even after accounting for the uncertainty in prevalence. 10.1371/journal.pgen.1002141.t004 Table 4 Heritability estimates. Source Description NINDS All PD - 0.229 (0.000–0.543) 0.833 (0.500–0.935) 0.077 (0.036- ) 23andMe All PD - 0.272 (0.229–0.315) 0.857 (0.833–0.877) 0.065 (0.056–0.077) 23andMe Early-onset PD ( ) - 0.306 (0.136–0.476) 0.873 (0.766–0.933) 0.057 (0.037–0.129) 23andMe Late-onset PD ( ) - 0.285 (0.224–0.346) 0.863 (0.830–0.890) 0.062 (0.051–0.078) [12] Twin study; broad-definition PD - 0.30 (0.00–0.47) 0.87 (0.50–0.93) 0.059 (0.037- ) [10] Twin study; all PD - 0.274 (0.000–0.708) 0.858 (0.000–0.976) 0.064 (0.025- ) [10] Early-onset PD ( ) - 1.0 (0.33–1.00) 0.996 (0.884–0.996) 0.018 (0.018–0.053) [10] Late-onset PD ( ) - 0.068 (0.00–0.59) 0.693 (0.000–0.958) 0.258 (0.030- ) [48] Family study; all PD - 0.401 0.910 0.044 [48] Early-onset PD ( ) - 0.169 0.793 0.104 [48] Late-onset PD ( ) - 0.453 0.926 0.039 [73] Family study; all PD - 0.60 (0.40–0.80) 0.96 (0.91–0.99) 0.029 (0.022–0.044) [14] Offsprings; all PD 3.0 0.35 0.89 0.050 [14] Late-onset PD ( ) 3.2 0.38 0.90 0.046 [74] Parents and siblings; all PD 3.92 0.456 0.927 0.038 [74] Early-onset PD ( ) 7.76 0.747 0.980 0.024 [74] Late-onset PD ( ) 2.95 0.348 0.891 0.050 denotes the heritability of liability for PD, with a 95% CI provided where available. In the case of [10], confidence intervals were estimated via a bootstrap procedure based on numbers provided in the original paper. For studies that did not provide direct estimates of heritability, the relative recurrence risk ratio was used to estimate under the assumption of no shared environmental covariance (see Materials and Methods). denotes the maximum theoretical AUC corresponding to the given heritability of liability, assuming a disease prevalence of 0.01. denotes the proportion of additive genetic variance explained by a genetic profile that achieves an AUC of 0.6 (see Materials and Methods). Risk prediction Given our estimates of the genetic contribution to PD, we then sought to determine the proportion of this contribution that we could attribute to specific genetic factors on our genotyping panel by constructing risk prediction models for PD. We considered two settings: an internal five-fold cross-validation experiment, where we divided the 23andMe cohort into five matched sets of cases and controls and computed predictions for each set using models trained using the other four sets; and an external cross-validation experiment, where we trained risk prediction models using the entire 23andMe cohort and tested them on the NINDS cohort after restricting both datasets to the set of common SNPs passing quality control for each dataset individually. In both the internal and external validation experiments, we measured the discriminative accuracy of the risk prediction algorithm using the area under the receiver operating characteristic curve (AUC). The AUC for a model can be interpreted as the probability that a randomly selected case will have a higher estimated risk of developing PD than a randomly selected control. An AUC of 1 implies that a model discriminates perfectly between cases and controls, whereas an AUC of 0.5 corresponds to a model based on random guessing. To measure predictive accuracy, we used a covariate-adjusted measure of AUC that removed the effect of potential confounding by sex, age, population structure, and, where appropriate, cross-validation fold or genotyping platform (see Materials and Methods). To avoid making manual decisions in the choice of SNPs to include, we used a sparse logistic regression algorithm for building risk prediction models, and varied the strength of the sparsity-inducing prior (see Materials and Methods). For a given training set, this procedure generated a series of risk prediction models of differing size, each of which we characterized using an approximate theoretical upper bound on the expected number of false positive SNPs, ; here, corresponds to a model containing only genome-wide significant associations. In the internal five-fold cross-validation experiment (see Table 5), the differences in AUCs between each of the largest three models (i.e., , , or ) and each of the smallest two models (i.e., or ) were significant (e.g., comparing the largest and smallest models, one-sided ; see Table S7). In the external cross-validation results, the four largest models were significantly better than the genome-wide significant model (e.g., comparing the largest and smallest models, one-sided ). 10.1371/journal.pgen.1002141.t005 Table 5 Internal and external cross-validation experiments using sparse logistic regression. Internal Validation External Validation Signif. Threshold Avg SNPs Avg Regions AUC SNPs Regions AUC 9.0 6.6 11 9 18.4 15.4 22 19 41.6 35.0 60 51 156.0 138.8 220 195 698.4 639.2 803 727 The internal five-fold cross-validation experiment was performed using only the 23andMe cohort. The external cross-validation experiment was performed by training on the 23andMe cohort and testing on the NINDS cohort. “SNPs” denotes the number of SNPs included in the fitted model. “Regions” denotes the number of distinct LD blocks represented by the SNPs in the fitted model. Each AUC value represents a covariate-adjusted AUC. For the internal validation experiment, average values are provided for SNPs and Regions, providing an average over all five cross-validation folds, and AUCs were computed by pooling predictions over the five cross-validation folds. For each row of the table, the sparsity inducing prior was chosen to achieve the approximate upper bound on the expected false positive rate indicated in the first column; here, corresponds to a model containing only genome-wide significant associations, whereas corresponds to suggestive associations. In each of the internal and external validation experiments, models with AUCs in bold are significantly better than non-bold models (see Table S3). Taken at face value, these results seem to suggest that the larger models, which include many more genomic regions than those deemed genome-wide significant, may harbor associations that account for their increased predictive accuracy. An alternative possibility, however, is that the differences in performance between models are actually just a consequence of differing levels of bias arising from the use of sparsity-inducing regularization. In Text S1 and Table S4, we present an argument using a bias-corrected version of our external cross-validation experiment that the above caveats do not explain the improved accuracy for the and models, thus suggesting that these models are likely to harbor additional important loci for PD; see Tables S5 and S6 for the SNPs included in these models. We note that this argument may not be the only way of demonstrating the existence of meaningful associations beyond the genome-wide significance threshold; closely related arguments based on the sparse regression methods [32] or genetic profile scores have also been previously proposed [33]. Regardless, our heritability estimates imply an upper bound on AUC for a genetic risk prediction model of roughly 0.83 to 0.88 based on the method of [31], though this would rise if the actual heritability were higher. Based on these numbers, the genetic risk prediction models detailed previously, which attain an AUC of roughly 0.6 in our cross-validated tests, account for approximately – of the total genetic variance in liability (see Materials and Methods). Discussion We found two novel associations at a genome-wide level of significance near SCARB2 (rs6812193) and SREBF1/RAI1 (rs11868035), both of which were replicated in data from [23]. We also report two novel associations (near RIT2 and USP25) just under the level of significance, one of which (RIT2) was also replicated. While it is difficult to pinpoint any causal genes from a GWAS, there are a few biologically plausible candidates worthy of discussion. The PD-associated SNP rs6812193 lies in an intron of the FAM47E gene, which gives rise to multiple alternatively spliced transcripts, many of which are protein-coding; the functions of these hypothetical proteins are unknown. A more attractive candidate, located kb centromeric to the SNP, is SCARB2 (scavenger receptor class B, member 2), which encodes the lysosomal integral membrane protein type 2 (LIMP-2). LIMP-2 deficiency causes the autosomal-recessive disorder Action Myoclonus-Renal Failure syndrome (AMRF), which combines renal glomerulosclerosis with progressive myoclonus epilepsy associated with storage material in the brain [34]. LIMP-2 is involved in directing -glucocerebrosidase to the lysosome where it hydrolyzes the -glycosyl linkage of glucosylceramide [35]. Deficiency of this enzyme due to mutations in its gene (GBA) causes the most common lysosomal storage disorder, Gaucher's disease. Recently, mutations in GBA have also been identified in PD [36], pointing to a possible functional link between the newly identified candidate gene SCARB2 and PD. rs11868035 appears in an intron of the alternatively spliced gene, SREBF1 (sterol regulatory element-binding transcription factor 1), within the Smith-Magenis syndrome (SMS) deletion region on 17p11.2. SREBF1 encodes SREBP-1 (sterol regulatory element-binding protein 1), a transcriptional activator required for lipid homeostasis, which regulates cholesterol synthesis and its cellular uptake from plasma LDL [37]. Studies of neuronal cell cultures have implicated SREBP-1 as a mediator of NMDA-induced excitotoxicity [38]. rs11868035 is directly adjacent to the acceptor splice site for the C-terminal exon of the SREBP-1c isoform of the protein [39], suggesting that the effect of the polymorphism may be specifically related to the splicing machinery for this protein. The mutation is also in strong LD with rs11649804, a nonsynonymous variant in the nearby gene RAI1 (retinoic acid-induced protein 1), which regulates transcription by remodeling chromatin and interacting with the basic transcriptional machinery. Heterozygous mutations in RAI1 reproduce the major symptoms of SMS, such as developmental and growth delay, self-injurious behaviors, sleep disturbance, and distinct craniofacial and skeletal anomalies [40]. Future work is needed to identify the functionally important variant(s) responsible for this association. The SNP rs4130047, slightly below the genome-wide significance threshold, lies in an intron of the RIT2 (Ras-like without CAAX 2) gene that encodes Rit2, a member of the Ras superfamily of small GTPases. Though we do not claim this SNP as a confirmed replication, there are a number of reasons to suspect that this association may also be real. Rit2 binds calmodulin in a calcium-dependent manner, and is thought to regulate signaling pathways and cellular processes distinct from those controlled by Ras [41]. It localizes to both the nucleus and the cytoplasm. Independent of our study, RIT2 was previously proposed as a candidate gene for PD, based on the possibility that dopaminergic neurons may be especially vulnerable to high intracellular calcium levels, perhaps through an interaction with -synuclein [42]. The PD-associated region contains another biologically plausible candidate gene, SYT4 (synaptotagmin IV), which encodes synaptotagmin-4, an integral membrane protein of synaptic vesicles thought to serve as sensor in the process of vesicular trafficking and exocytosis. It is expressed widely in the brain but not in extraneural tissues [43]. Homozygous Syt4−/− mouse mutants have impaired motor coordination [44]. SYT4 is particularly interesting as a SNP near SYT11 (synaptotagmin XI) has been associated with PD in [22], and the encoded protein, synaptotagmin-11, is known to interact with parkin [45]. The suggestively associated SNP rs28233572 lies in a gene-poor region with only one candidate gene downstream, USP25, encoding ubiquitin specific peptidase 25, which regulates intracellular protein breakdown by disassembly of the polyubiquitin chains. Other ubiquitin-specific proteases (USP24, USP40) have been proposed as candidate genes for PD [46] (although USP24 fails to replicate here, see Table 3). Our heritability estimates, which suggest that genetic factors account for at least one-fourth of the total variation in liability to PD, represent the tightest confidence bounds determined for the heritability of PD to date. These estimates, which rely on observed genetic sharing rather than predicted relationship coefficients, avoid confounding from shared environmental covariance by restricting attention to very distantly related individuals. Furthermore, they complement estimates of heritability from twin studies by considering large numbers of individuals with low amounts of genetic sharing, rather than small numbers of twin pairs with large amounts of genetic sharing. These estimates should only be interpreted as lower bounds on the actual heritability of liability of PD for two reasons. First, they only reflect phenotypic variation due to causal variants in LD with SNPs on the genotyping platform. Second, they only capture the contribution to additive variance that arises from a polygenic model of many SNPs of small effect, but do not include the variance arising from known specific associations. This limitation is most apparent in our estimate of heritability based on only early-onset cases ( ), which is considerably lower than reported in prior twin studies (e.g., in [10]). In early-onset PD, mutations in six specific genes (SNCA, PRKN, PINK1, DJ1, LRRK2, and GBA) have been reported to account for 16% of cases [47]; these specific mutations are not directly accounted for in our estimate, which is based on a polygenic model. We note that a similar effect may explain the low heritability estimate for early-onset PD in [48]. Thus, the actual heritability of PD, and the corresponding true upper bound on discriminative accuracy achievable through genetic factors, may be even higher than the estimates we provide. Our estimates also indicate a substantial genetic component for late-onset PD ( ), for which previous estimates of heritability have been inconclusive due to the lack of statistical power (e.g., 0.068 in [10] and 0.453 in [48]). One might ask, if late-onset PD is indeed so heritable, why do cases frequently appear sporadically in the general population? Following the analysis of [49], if one were to assume a heritability of and an average of three children per family, then the proportion of sporadic cases (i.e., no parent, child, sibling, grandparent, aunt or uncle, or first cousin with PD) among all PD cases would be 64% for a prevalence of ; in the 23andMe cohort, 69% of PD cases would be considered sporadic by this definition based on self-reported family history. Similarly, the expected proportion of PD cases with no affected parent or sibling would be 88% under the same assumptions, compared with 84% as reported in [50], or 89% based on the cohort in [51]. These examples illustrate the fact that the presence or absence of a familial pattern cannot always be used to determine pathogenesis, especially for diseases that are rare and have a complex etiology. Overall, our risk prediction results are consistent with a measured AUC of roughly 0.6. The cross-validated AUCs presented here should be distinguished from more usual measurements of AUC in genome-wide association studies, which are typically only estimated on the development set, and which rely on weighted combinations of SNPs with independently estimated odds ratios. In some cases, the bias resulting from lack of proper external validation can be quite large. For example, a simple genetic profile score based on multiplying together odds ratios for the SNPs in Table 2 appears to achieve an AUC of in the 23andMe data (or if no covariate adjustment is performed) making it appear competitive with some of the best models described in Table 5. However, when the same model is evaluated in the NINDS data, the AUC drops to , exhibiting a drop in performance characteristic of models that have been overfit to their training data. In contrast, the consistency between the internal and external validation results in the models shown in Table 5 demonstrate not only the predictiveness of our models within the 23andMe cohort but also their ability to generalize to other populations. Our empirical demonstration that including SNPs beyond the genome-wide significant level provides improved discriminative power mirrors the recent results of [32], which also studied the performance of sparse regression methods in a risk prediction setting. In an applied setting where the goal is to achieve the best predictive accuracy rather than to isolate the contribution of individual genetic factors, however, even higher discriminative accuracies may be possible if one were to incorporate these covariates as part of the predictive models. Even without these, however, significant improvements in risk prediction are likely still possible, with our heritability analyses indicating asymptotic target AUCs above 0.8. Our AUCs are generally conservative for a number of reasons. In the internal experiments, they were obtained by training on only 80% of the data. In the external experiments, the models included only the SNPs in common between the 23andMe and NINDS datasets and thus excluded several SNPs with large effects in LRRK2 and GBA that may add a percent or more to the AUC if included. Furthermore, our analyses adjusted for confounding from population structure and other covariates so as to ensure that the discriminative accuracies we reported were specifically due to genetic effects. Finally, we note that data for the 23andMe cohort used in this study were acquired in a novel manner, using genotype and survey data acquired through a commercial online personal genetic testing service. The use of self-reported phenotype data raised some unique challenges. For example, our cohort was not a true population sample for a number of reasons, such as the general bias toward higher socioeconomic status, as typical of 23andMe customers. In general, however, we would not expect these ascertainment biases to substantially affect our conclusions unless their effects varied differentially between the case and control sets. As another example, in compiling the cohort, we used participants with varying levels of completeness in their self-reported data (see Materials and Methods). Out of the 3,426 cases in the 23andMe cohort, though most cases reported having PD in a questionnaire, 482 affirmatively stated they had PD upon entry to the research study but did not fill out any PD-related questionnaire during the study. However, we did not see a large difference between those answering questions and not. Among the 11 associations presented in Table 2, only the association with MAPT showed a significant difference between the cohort who answered a questionnaire and those who did not (see Table S7). Also, approximately 84% of the cases filled out a questionnaire, and of them, over 96% reported a PD diagnosis. Even if a larger fraction (say 10–15%) of those who did not take a questionnaire did not have PD, the gain in power from the additional cases would more than offset the loss of power from having some 50 more false positive cases. Despite the challenges associated with using self-reported data collected through online surveys, ultimately, our results lend credibility to the accuracy of this novel research design. For example, the agreement between our study and previous studies in terms of the ORs estimated for the 19 associations replicated in Table 3 strongly suggests that our cohort is similar to those used in other PD studies. Similarly, the consistency of AUCs and heritability estimates across our cohort and the NINDS cohort both suggest a limited role of bias in our study. Importantly, our mode of data collection also provided a number of clear benefits. The use of internet-based techniques enabled rapid recruitment of a large patient community. The 3,426 cases in this study were enrolled in about 18 months, with over half joining in the first month of the study. Also adding significantly to the power and robustness of this study was the availability of a large cohort of controls derived from the 23andMe customer base. By using a non-traditional recruitment approach, we thus were able to attain good power for our study through large sample sizes. To our knowledge, this study represents the largest genome-wide association study of Parkinson's disease conducted on a single cohort to date, with only a recent meta-analysis achieving a larger number of cases [22]. We suggest that this methodology for study design may prove advantageous for other conditions where the advantage of having a large cohort is paramount for detecting subtle genetic effects. In summary, we have for the first time used a rapid, web-based enrollment method to assemble a large population for a genome-wide association study of PD. We have replicated results from numerous previous studies, providing support for the utility of our study design. We have also identified two new associations, both in genes related to pathways that have been previously implicated in the pathogenesis of PD. Using cross-validation, we have provided evidence that many suggestive associations in our data may also play an important role. Using recently developed analytic approaches developed for GWAS that take into account the ascertainment bias inherent in a case-control population, we have estimated the genetic contribution to PD in this sample. These findings confirm the hypothesis that PD is a complex disorder, with both genetic and environmental determinants. Future investigations, expanded to include environmental as well as genetic factors, will likely further refine our understanding of the pathogensis of PD, and, ultimately, lead to new approaches to treatment. Materials and Methods Study populations The 23andMe cohort consisted of customers of 23andMe, Inc., a personal genetics company. Patients with PD were recruited to join this cohort through a targeted email campaign in conjunction with the Michael J. Fox Foundation, The Parkinson's Institute and Clinical Center, and many other PD patient groups and clinics. Emails or hard copy mailings were sent to all individuals who had registered with these groups as PD patients. A limited number of patients were also recruited in person at PD workshops and conferences. Family members of individuals with the LRRK2 G2019S were also recruited to participate in the general Parkinson's disease research at 23andMe, without regard to Parkinson's disease status; however, most of these individuals were not included in the cohort used for this particular study, due to our restriction of the dataset to unrelated individuals (see below). Patients were invited to fill out a screening questionnaire asking if they had been diagnosed with PD and their physician's name, phone number, and institution. Patients who stated they had been diagnosed with PD and who gave complete, non-suspicious answers to the other questions were offered the 23andMe Personal Genome Service for a nominal fee of $25. Individuals included in the 23andMe cohort were selected for being of primarily European ancestry, as determined through an analysis of local ancestry via comparison to the three HapMap 2 populations, using an unpublished method substantially similar to [52]. A maximal set of unrelated individuals in the 23andMe cohort was chosen for the analysis using a segmental identity-by-descent (IBD) estimation algorithm (as used in [53]). Individuals were defined as related if they shared more than 700 cM IBD, including both regions where the two individuals share either one or both genomic segments identical-by-descent. This level of relatedness (roughly 20% of the genome) corresponds approximately to the minimal expected sharing between first-cousins in an outbred population. We determined that 29 individuals were included in both the 23andMe and NINDS cohorts and hence were removed from the latter cohort for all analyses. Genotype and phenotype data for the National Institute of Neurological Disease and Stroke (NINDS) cohort were obtained from the NINDS Database found at http://www.ncbi.nlm.nih.gov/gap through dbGaP accession number phs000089.v3.p2, supplemented with individual-level data for 200 subjects from phs000089.v2.p2 who were left out of the later version as of December 12, 2010. Cases in the NINDS cohort consisted of North American Caucasians with Parkinson's disease, as assessed by a neurologist. Controls consisted of neurologically normal, unrelated, white individuals with no family history for a number of neurological conditions, including Parkinson's disease. A complete description of the inclusion and exclusion criteria can be found directly at the NINDS Database website as referenced above, and in related studies using the data from this cohort [16], [54], [55]. This study was conducted according to the principles expressed in the Declaration of Helsinki. The 23andMe study protocol and consent were approved by the external AAHRPP-accredited IRB, Ethical and Independent Review Services (E&I Review). Our consent and privacy statement preclude the sharing of individual-level data without explicit consent. We have, however, shared summary statistics for all SNPs with -values under (Table S2). We also hope to further collaborate with the scientific community using this data. The NINDS dataset was analyzed anonymously. Self-reported diagnosis Patients recruited through the PD outreach initiative as well as individuals from the general 23andMe customer base were asked to take online questionnaires, including a general medical questionnaire and a detailed questionnaire specifically on PD (covering disease onset, diagnosis, and symptoms). Both of these questionnaires asked the subject if he or she had ever received a PD diagnosis from a physician and if so, the age of onset. The detailed questionnaire also asked for much more specific information regarding the symptoms, clinical history, and family history of the patient. We selected as cases all participants who provided an affirmative diagnosis of PD from a physician (on the initial screening form or on either of the two questionnaires) and who did not provide any potentially contradictory information, defined here as: Providing an affirmative answer to the screening question but only negative answers to the two questions about PD. Answering “yes” to PD on the general medical questionnaire but “no” to PD on the detailed questionnaire. Stating their diagnosis changed because they no longer had symptoms or because the cause of their symptoms was unknown. Stating they had been diagnosed with any of 19 other neurological conditions (see Table S8). Due to the low prevalence of PD, we used controls taken from general 23andMe customer base in the analysis. Some of the controls filled out no questionnaires; however, others answered questions about possible PD-like symptoms or filled out a general medical history. In order to maximize our power to detect genetic associations with PD, we excluded some putative controls who might be at higher probability for developing PD in the future. Thus, the controls consisted of all consented European 23andMe customers who met all of the following criteria: Were not part of a PD related recruitment drive ( 130 individuals excluded) Did not report a diagnosis of PD, Parkinsonism, dementia, cognitive impairment, senility, tremor disorder, Alzheimer's disease or memory loss ( 240 individuals excluded) Did not report a family history of PD ( 780 individuals excluded) Reported a maximum of two of the following PD-like symptoms ( 280 individuals excluded): Trembling or shaking of any body part Handwriting became slower, smaller, or shakier (each considered a separate symptom) Speech or voice become softer Dragging one or both feet while walking Feet shuffling while walking Walking more slowly Taking smaller steps than before Steps becoming faster and faster Feet getting stuck as if glued to the floor Swinging arms less than before Stooping or bending forward more than before Falling or balance trouble Approximately 1,430 individuals in total were excluded from the control set due to these filters. We note that as a consequence of both our exclusion criteria and other recruitment biases associated with the 23andMe customer base, our controls are unlikely to be exactly representative of the general population. Genotyping and SNP quality control For the 23andMe cohort, DNA extraction and genotyping were performed on saliva samples by National Genetics Institute (NGI), a CLIA-certified clinical laboratory and subsidiary of Laboratory Corporation of America. Samples were genotyped on the Illumina HumanHap550+ BeadChip platform, which included SNPs from the standard HumanHap550 panel augmented with a custom set of approximately 25,000 SNPs selected by 23andMe. Every sample that failed to reach 98.5% call rate was re-analyzed. Individuals whose analyses failed repeatedly were re-contacted by 23andMe customer service to provide additional samples, as is done for all 23andMe customers. Two slightly different versions of the genotyping platform were used in this study. See [53] for further details on the genotyping and sample quality controls. The NINDS dataset consisted of 519 samples genotyped on a combination of an Illumina HumanHap 250 K and Illumina HumanHap 300 K chip, and 1,183 samples genotyped on an Illumina HumanHap 550 K chip. As the proportion of cases genotyped on each platform in the NINDS dataset differed between the two platforms, any marker with differing frequencies across the two platforms (due to problems with clustering or other genotyping error) would show up as associated with PD status in the NINDS dataset. To account for potential stratification arising from this, we defined a binary covariate to indicate genotyping platform, which we used for covariate adjustment during analyses involving the NINDS dataset. In all analyses, SNPs with a call rate or minor allele frequency were excluded from analysis. Additionally, SNPs with Hardy-Weinberg -values or were excluded from the 23andMe and NINDS datasets, respectively [56]. For analyses involving external validation of risk prediction models trained on the 23andMe dataset against the NINDS dataset, only SNPs common to both datasets were used in both model development and testing. Altogether, 522,782 SNPs were retained for the 23andMe dataset with an average call rate of 99.8%, 514,362 SNPs were retained for the NINDS dataset with an average call rate of 99.8%, and 492,136 SNPS were common to both datasets. Association analysis For the association analysis, all -values were calculated using a likelihood ratio test for the logistic regression model, adjusting for sex, age, and the first five principal components (chosen based on an examination of the eigenspectrum of our data): Here, the phenotypic status of each individual was coded as for unaffected individuals and 1 for affected individuals. Genotypes were coded to indicate the number of minor alleles present for tested SNP (corresponding to a log-additive model of association), and was the projection of the individual onto the th principal component of the genotype data matrix. Reported odds ratios for each SNP relative to the minor allele were defined as , and the alleles used throughout refer to the plus strand of NCBI build 36.3 of the human genome. Principal components were computed using multi-dimensional scaling over the allele-sharing distance matrix as in [53]. The SNPs used for the replication analysis (Table 3) were taken from http://www.pdgene.org/ [27] and http://www.genome.gov/gwastudies/ [57] on November 18, 2010. We added the SNPs reported as genome-wide significant from [22] to this list. For the power calculations, we used the model from [58]. Heritability estimation To estimate heritability of liability, we used the GCTA package (v0.90.3) [29] for genome-wide complex trait analysis. Previously, this approach was used to estimate the proportion of the heritability in height that could be explained by common variation on a genomic panel [69]. Here, we used a recent adaptation of this method to case-control studies [30] to estimate the heritability of PD in both the NINDS and 23andMe cohorts. We analyzed the NINDS cohort data by using GCTA to remove individuals with genetic relationship greater than 0.025, and estimating heritability of liability using 20 principal components as covariates and assuming a disease prevalence of 0.01. For the 23andMe cohort, we adopted the same procedure but pre-filtered the data by stratifying the dataset on sex, and matching on age and five principal components in order to obtain a reduced size dataset with one case per four controls. For Table 4, we converted relative recurrence risk ratios to heritability of liability estimates using a modification of the analysis described in [31]. Formulas for estimating the maximum AUC achievable for a given heritability, and for computing the proportion of variance in liability explained were also based on [31]. Details are provided in Text S1. We note that in Table 4, the heritability estimates shown were based on the authors' criteria for “broad-definition PD” as no heritability estimates could be provided for the strict PD definition due to the lack of concordant monozygotic twins present in the dataset. For [10], 95% confidence intervals were obtained through a reanalysis of the original data using 100,000 bootstrap samples for the counts of doubly-ascertained concordant, singly-ascertained concordant, and discordant monozygotic and dizygotic twin pairs. Heritability of liability was estimated as twice the difference in tetrachoric correlations for monozygotic and dizygotic twins, using a specialized numerical integration procedure for multivariate normal densities [70]. Risk prediction We performed risk prediction experiments using a sparse logistic regression solver based on the “elastic net” regularization penalty [59]. In this approach, one solves the convex optimization problem, for fixed constants , where and , and where . Sparse regression methods, which tend to estimate solution vectors with very few non-zero components, have enjoyed increased popularity in recent years due to their effectiveness in picking out relevant features from extremely high-dimensional data. In the context of genetic association analysis, sparse regression methods can be used to identify the set of SNPs that are most relevant to prediction of a given phenotype. The “elastic net” approach we used is a particular sparse regression variant based on combining / regularization penalties that has the advantage of grouping together correlated features while maintaining sparsity. We note that elastic net regularization has also previously been applied in the context of GWAS and SNP-based risk prediction in a number of recent papers [32], [60]–[62]. For all experiments, we used a default value of (to ensure uniqueness of the solution to the optimization problem) and evaluated the performance of the risk prediction algorithm in two different ways. We varied the hyperparameter to obtain different bounds on the expected number of false positive associations (i.e., genotype features with non-zero coefficients corresponding to SNPs that are not truly associated with the phenotype), using an adaptation of the analysis from [63]. AUC analysis We performed two types of cross-validation experiments: an internal cross-validation analysis using only the 23andMe cohort, and an external cross-validation analysis testing the predictive accuracy of a model trained using the 23andMe cohort on the NINDS cohort. In both cases, all aspects of the analysis following QC were included as part of the cross-validation. For the internal cross-validation experiment, we generated a matched dataset using a portion of the 23andMe cohort. More specifically, we separated the 23andMe dataset into 20 partitions based on sex and age decile. Next, all partitions were then balanced to contain roughly the same ratio of cases to controls. Finally, five equally-sized cross-validation folds were formed, containing the same amount of representation from each of the partitions. In total 3,380 cases and 21,640 controls were used across the five cross-validation folds. For the external cross-validation experiment, the entire 23andMe cohort was used as a training set, and evaluation was performed on the NINDS dataset. When estimating AUC using a test set, stratification biases can arise when the apparent discriminative accuracy of the model can be attributed to one or more covariates. This could occur, for example, if the prevalence of the disease were to vary by population, provided that the SNPs included in the risk prediction model were informative of ancestry. To control for confounding from covariate imbalance, we used a stratified variant of the AUC known as the “covariate-adjusted AUC,” defined as the probability that a randomly selected case will have a higher estimated risk of developing PD than a randomly selected matched control. More details on our procedure for covariate adjustment are provided in Text S1. The use of AUC-based statistics for risk prediction is not without controversy. In the setting of a case-control study, the AUC has the advantage of being neither dependent on an arbitrarily set threshold for risk (which would be needed when computing sensitivity or specificity) or the relative proportion of cases and controls in the study. Some authors have contended that the AUC is not a clinically relevant measurement of performance and may be insensitive to changes that would otherwise be considered important in a diagnostic setting [64]–[67], while others have argued that changes in AUC are nonetheless meaningful in assessing discriminative performance [68]. Here, we have chosen to rely on AUC not as a summary of the clinical performance of a classifier, but rather as a mechanism for studying the genetic etiology of a disease, and for estimating the proportion of genetic variance captured by the SNPs used in our models. Were one specifically interested in developing a clinically useful classifier, other measures of accuracy may be more appropriate. Since the goal of our experiments was to measure the predictive capacity that could be attributed to SNPs in our model, rather than covariates such as sex, age, or ancestry, we intentionally excluded covariates when fitting our predictive models. We note that because of our use of covariate-adjusted AUCs, the decision to exclude covariates had little impact on our results since changes in predictive performance arising from the inclusion of covariates would have been “factored out” by the stratification procedure anyway. For example, the covariate-adjusted external validation accuracies of the smallest and largest models in Table 5 were 0.550 and 0.605, respectively; the analogous risk prediction model including covariates would have achieved accuracies of 0.557 and 0.603. Supporting Information Figure S1 Manhattan plot -values by chromosome for the 23andMe dataset. Genome-wide significant SNPs are shown in red. (TIFF) Click here for additional data file. Figure S2 Quantile-quantile plot Observed -values versus theoretical -values under the null. The genomic control inflation factor for the study was and is shown by the red line. (TIFF) Click here for additional data file. Figure S3 Plot of -values around RIT2/SYT4. Colors depict the squared correlation ( ) of each SNP with rs4130047. For details, see Figure 1. (TIFF) Click here for additional data file. Figure S4 Plot of -values around rs2823357 and USP25. Colors depict the squared correlation ( ) of each SNP with rs2823357. For details, see Figure 1. (TIFF) Click here for additional data file. Table S1 Genotype by phenotype tables for SNPs in Table 2. (PDF) Click here for additional data file. Table S2 Details for all SNPs with -values under . See Table 2 for details. (XLS) Click here for additional data file. Table S3 Internal and external cross-validation AUC difference test for sparse logistic regression models. Rows and columns of each table correspond to models being compared, and are labeled using the theoretical upper bound on of the model for that particular row or column. Elements of the tables are one-sided -value tests for the alternative hypothesis that the row model has a higher AUC than the column model. One-sided comparisons significant at the 0.05 level are indicated in bold. (PDF) Click here for additional data file. Table S4 External cross-validation AUC difference test using bias-corrected models. Each row of the table represents a comparison of a “test” risk prediction model based on the significance threshold indicated in the first column against a “reference” model containing only SNPs found in genome-wide significant regions. In all cases, reported AUCs have been adjusted for covariates (see Materials and Methods), and all models were bias-corrected by omitting the sparsity-inducing prior during model fitting. The second and third columns show the predicted AUC for each model based on the estimated SNP effect sizes and test distribution genotype frequencies. The fourth and fifth column show the covariate-adjusted AUCs actually observed on the test data. The poor agreement between predicted and observed test AUC for the largest two models is evidence of severe overfitting in these cases. The last column gives one-sided -values for an AUC difference test under the alternative hypothesis that the test model has a higher AUC than the reference model; one-sided comparisons nominally significant at the 0.05 level are indicated in bold. (PDF) Click here for additional data file. Table S5 Bias-corrected model. This model, which achieves a covariate-adjusted AUC of 0.608 on the NINDS data, was obtained by training on the 23andMe cohort, using the subset of SNPs that were shared with the NINDS cohort. refers to the weight for each SNP (i.e., the log odds ratio per copy of the alphabetically lesser allele), and is the weight used in the algorithm in the case of missing data for that SNP. (PDF) Click here for additional data file. Table S6 Bias-corrected model. This model, which achieves a covariate-adjusted AUC of 0.614 on the NINDS data, was obtained by training on the 23andMe cohort, using the subset of SNPs that were shared with the NINDS cohort. refers to the weight for each SNP (i.e., the log odds ratio per copy of the alphabetically lesser allele), and is the weight used in the algorithm in the case of missing data for that SNP. (PDF) Click here for additional data file. Table S7 Test for heterogeneity. The low confidence group consisted of participants who did not answer a questionnaire, whereas the high confidence group consisted of participants who did. The second and third columns show the estimated log odds-ratio for each SNP from Table 2 using only low and high confidence data, respectively. The fourth column shows the combined log odds-ratio when using data from both groups together, and the final column gives a -value for heterogeneity. Note that while three of the -values are nominally significant, only that for rs12185268 survives a correction for multiple testing (correcting for the 11 SNPs tested). (PDF) Click here for additional data file. Table S8 Exclusionary conditions. People reporting any of the above diagnoses were excluded from the analysis. (PDF) Click here for additional data file. Text S1 (PDF) Click here for additional data file.
Author and article information
Journal
Journal ID (nlm-journal-id): 9216904
Journal ID (pubmed-jr-id): 2419
Journal ID (nlm-ta): Nat Genet
Journal ID (iso-abbrev): Nat. Genet.
Title:
Nature genetics
ISSN
(Print):
1061-4036
ISSN
(Electronic):
1546-1718
Publication date Nihms-submitted: 19
December
2014
Publication date
(Electronic):
02
February
2015
Publication date
(Print):
March
2015
Publication date PMC-release: 01
September
2015
Volume: 47
Issue: 3
Pages: 284-290
Affiliations
[2
]Program in Medical and Population Genetics, Broad Institute of Harvard and MIT, Cambridge,
Massachusetts, USA.
[3
]Department of Mathematics, Massachusetts Institute of Technology, Cambridge, Massachusetts,
USA.
Author notes
Correspondence should be addressed to P.-R.L. (
loh@
123456hsph.harvard.edu
) or A.L.P. (
aprice@
123456hsph.harvard.edu
)
Article
Manuscript ID: NIHMS650284DOI: 10.1038/ng.3190
PMC ID: 4342297
PubMed ID: 25642633
SO-VID: 8b3f0fdc-f615-44bd-a94b-7107e258f893
History
Categories
Subject:
Article
ScienceOpen disciplines: Genetics
Data availability:
ScienceOpen disciplines: Genetics